机器学习算法系列(三):最大熵模型

作者 | Ray
编辑 | 安可
出品 | 磐创AI技术团队
目录:
一、熵与条件熵
二、最大熵模型的思想
三、最大熵模型的定义
四、最大熵模型损失函数的优化求解
五、最大熵模型的优缺点
一、熵与条件熵
熵度量的是事物的不确定性。越不确定的事物,它的熵就越大。具体的,随机变量熵的表达式为:
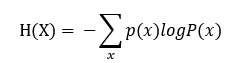
且熵满足下列不等式:
0≤H(P)≤log|X|
其中|X|为X的取值个数。当且仅当X的分布为均匀分布的时候,右边等号成立。因为当X为均匀分布, X的每种取值的可能性都一样,这种情况不确定性最大,因而对应的熵也最大。
条件熵公式为:
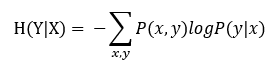
二、最大熵模型的思想
最大熵模型认为,学习概率模型时,在所有可能的概率模型中,熵最大的模型是最好的模型。若模型要满足一些约束条件时,则最大熵原理就是在满足已知条件的概率模型集合中,找到熵最大的模型。因而最大熵模型指出,在预测一个样本或者一个事件的概率分布时,首先应当满足所有的约束条件,进而对未知的情况不做任何的主观假设。在这种情况下,概率分布最均匀,预测的风险最小,因此得到的概率分布的熵是最大。
很显然,最大熵模型的思想是合理的。接下来,将通过一个例子来说明。假设随机变量X有5个取值{A,B,C,D,E},如果约束条件为P(A)+ P(B)+ P(C)+ P(D)+ P(E)=1。在没有其他任何信息的情况下要估计各个值的概率时,我们只能估计为等概率,即P(A)=P(B)=P(C)=P(D)=P(E)=1/6。且这种判断是合理的。若我们除此之外还有了其他约束条件时,如:P(A)+P(B)=3/10,那么我们可以认为A与B等概率,C、D、E是等概率的。
可以发现以上的概率估计方法遵循了的恰恰是最大熵的原理。
三、最大熵模型的定义
最大熵模型假设分类模型是一个条件概率分布P(Y|X),X为输入特征,Y为类标。给定一个数据集
T ={(x1,y1),(x2,y2),…,(xn,yn)}
学习的目标就是用最大熵模型选择一个最好的模型。
在给定训练集的情况下,我们可以得到总体联合分布P(X,Y)的经验分布和边缘分布P(X)的经验分布,即:
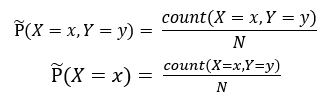
用特征函数f(x,y)表示x和y之间的关系,即上文所说的约束条件。
则可以得到:
特征函数 f(x,y) 关于经验分布(X,Y) 的期望值为:
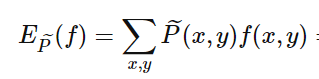
特征函数 f(x,y) 关于经验分布(X)与P(Y|X)的期望值为:
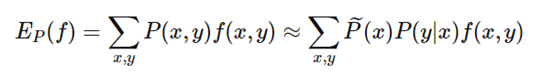
经验分布与特征函数结合便能代表概率模型需要满足的约束,只需使得两个期望项相等, 即:
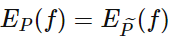
或:
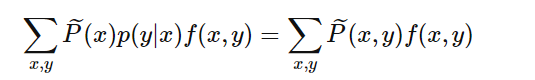
我们将上式作为模型学习的约束条件。假如有n个特征函数,那么就有n个约束条件。
这样最大熵模型的定义如下:
假设满足所有约束条件的集合为:
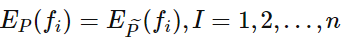
定义在条件概率分布P(Y|X)上的条件熵为:
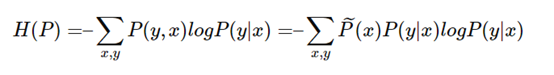
我们的目标就是找到使得H(P)最大的时候所对应的P(y|x),这里可以对H(P)加了个负号求极小值,这样做的目的是为了使−H(P)为凸函数,方便使用凸优化的方法来求极值。
因此最大熵的的损失函数为:
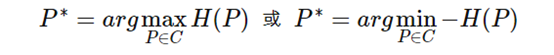
四、最大熵模型损失函数的优化求解
通过上一节的定义,我们给出最大熵模型的目标函数为:
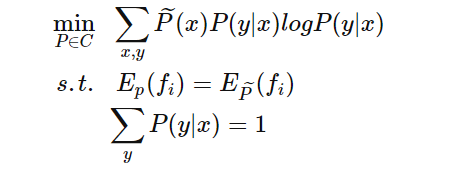
最大熵模型的目标函数是带有约束的最优化问题,根据上一篇文章拉格朗日对偶性的学习,可以将这个问题转化为无约束最优化的问题。
首先,引进拉格朗日乘子w0,w1,…,wn,定义该函数对应的拉格朗日函数:

最优化的原始问题为:
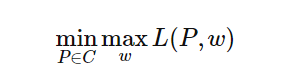
对偶问题是:
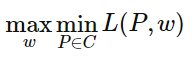
首先求解对偶问题内部的极小化问题minL(P,w),得到的解是关于w的函数,将其记作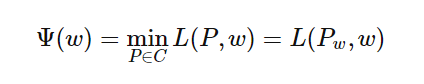
上式的解可以记作:
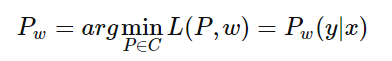
要求得Pw只需对P(y|x)求导即可,令导数为0即可得到:
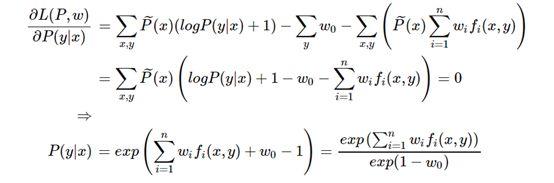
因为:
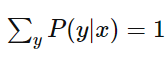
可得:
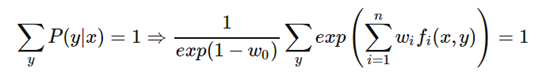
进而得到:
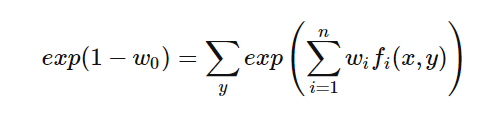
这里exp(1-w0)起到了归一化的作用,令Zw(x)表示exp(1-w0),得到:
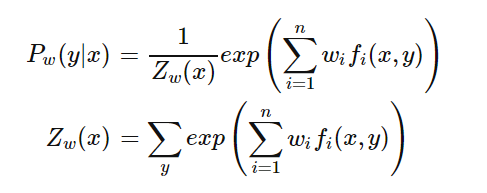
这样我们就得出了P(y|x)和w的关系,从而可以把对偶函数ψ(w)里面的所有的P(y|x)替换成用w表示,这样对偶函数ψ(w)就是全部用w表示了。接着我们对ψ(w)求极大化,就可以得到极大化时对应的w向量的取值,带入P(y|x)和w的关系式,从而也可以得到P(y|x)的最终结果。
对ψ(w)求极大化,由于它是连续可导的,所以优化方法有很多种,比如梯度下降法,牛顿法,拟牛顿法都可以。对于最大熵模型还有一种专用的优化方法,叫做改进的迭代尺度法。
五、最大熵模型的优缺点
优点:
1. 最大熵统计模型获得的是所有满足约束条件的模型中信息熵极大的模型,作为经典的分类模型时准确率较高。
2. 可以灵活地设置约束条件,通过约束条件的多少可以调节模型对未知数据的适应度和对已知数据的拟合程度。
缺点:
1. 由于约束条件的个数往往是跟样本的数量有关,因此当样本数量越来越多的时候,对应的约束条件也会相应增加,这样就会导致计算量越来越大,迭代速度越来越慢,这在实际应用中很难。

你也许还想看:
欢迎扫码关注:
原创文章,作者:fendouai,如若转载,请注明出处:https://panchuang.net/2019/01/28/a9f184fb2c/



