一文带你实战强化学习（下） | DQN

作者 | 小猴锅

编辑 | 奇予纪

出品 | 磐创AI团队出品

【磐创AI导读】：本篇文章是深度强化学习专栏的第四篇，讲了第五节实战强化学习中Monte Carlo Policy Gradient 算法及Actor Critic 算法，希望对大家有所帮助。查看关于本专栏的介绍：深度强化学习（DRL）专栏开篇。想要获取更多的机器学习、深度学习资源，欢迎大家点击上方蓝字关注我们的公众号：磐创AI。

目录：

1. 引言

2. 强化学习基础知识

3. 有模型的强化学习方法

4. 无模型的强化学习方法

5. 实战强化学习算法

Q-learning 算法
Monte Carlo Policy Gradient 算法
Actor Critic 算法

6. 深度强化学习算法

7. 专栏小结

5.2 Monte Carlo Policy Gradient算法

“CartPole-v1”是Gym中一个控制类的游戏，如图左所示。一根杆子的一端连接在一个小车上，由于重力的原因，杆子会发生倾斜，当杆子倾斜到一定程度后就会倒下，游戏任务就是通过左右移动底部的小车来保持杆子竖直向上，一旦杆子倒下游戏就结束了。

一文带你实战强化学习（下） | DQN

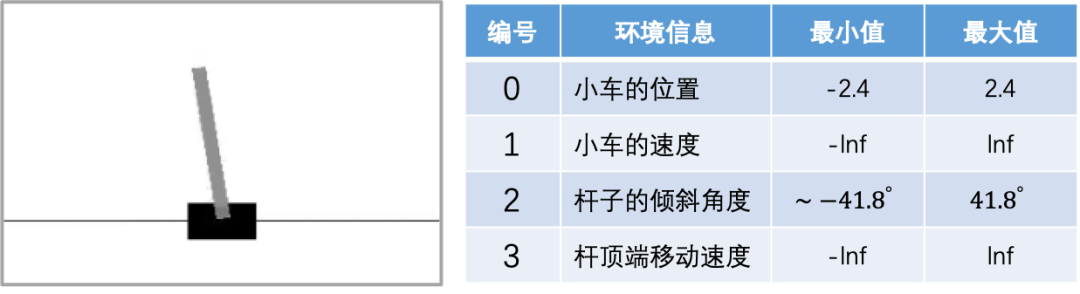
“CartPole-v1”游戏示意图

“CartPole-v1”游戏的环境状态由四部分组成，如图右所示。游戏中小车只有两个动作可以做，分别是向左移动和向右移动（其值分别为0和1）。每做一次动作，如果杆子没有倒下，则得到奖励值1。

根据蒙特卡洛策略梯度（Monte Carlo Policy Gradient）算法，我们需要有一个可微分的策略函数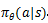一文带你实战强化学习（下） | DQN 。“CartPole-v1”游戏只有两个动作，因此我们可以简单的把它看成一个二分类问题，在第三章内容里我们介绍激活函数的时候提到的Sigmoid型函数正好可以用在这里，我们选择最简单的Logistic函数作为我们的策略函数：

一文带你实战强化学习（下） | DQN

式3

Logistic函数只有一个变量x，“CartPole-v1”的游戏环境由四个因素组成，如果我们全部考虑在内的话，那么我们的策略函数应当至少有4个参数，我们将其定义为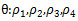一文带你实战强化学习（下） | DQN ，假设环境的四个因素分别为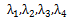，则我们令Logistic函数中的变量x为：

一文带你实战强化学习（下） | DQN

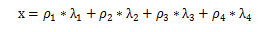
式4

选定策略函数之后，我们就可以实现使用策略来做动作选择的代码：

1  def policy_function(observation, theta):
2      # 根据当前的状态值和策略函数的参数值计算策略函数的输出
3      x = np.dot(theta, observation)
4      s = 1 / (1 + np.exp(-x))
5      # 根据策略函数的输出进行动作选择
6      if s > 0.5:
7          action = 1
8      else:
9          action = 0
10      return s, action

在第3和第4行代码中，我们根据环境信息（小车的位置、小车移动速度、杆子的倾斜角度以及杆子顶端的运动速度）和策略函数的参数值计算得到了策略函数的输出值（由于我们选择了Logistic函数作为策略函数，所以其值域为（0.1））,当策略函数的输出值大于0.5时，选择向右移动的动作，否则向左移动。

现在我们有了策略函数，也实现了由策略函数选择动作的代码，接下来我们需要考虑如何使用梯度的方式对策略函数的参数进行更新。根据蒙特卡洛策略梯度算法的描述，要实现对参数的更新，我们需要有一个完整的游戏“情节”，即一段完整的“episode”。我们定义一个获取“episode”的函数：

11  def generate_an_episode(env, theta):
12  # 定义一个数组用来保存整段“情节”
13      episode = []
14      # 重置游戏环境
15      pre_observation = env.reset()
16      # 定义一个变量，用来统计采取动作的次数
17      count_action = 0
18  
19      # 产生一个episode
20      while True:
21          # 根据策略选择动作
22          s, action = policy_function(theta, pre_observation)
23          # 执行选择的动作并得到反馈信息（新的环境状态、奖励等）
24          observation, reward, done, info = env.step(action)
25          # 保存这一步的信息
26          episode.append([pre_observation, action, s, reward])
27          # 更新环境状态
28          pre_observation = observation
29          # 累计执行的动作，当执行了超过5000次动作后，杆子还没倒下的话，主动结束游戏
30          count_action += 1
31          if done or count_action > 5000:
32              break
33      return episode

在第12行代码中我们定义了一个数组“episode”，用来保存agent在玩游戏时产生的整段“episode”中的每一步的信息。从第23行代码可以看到，“episode”数组的每一个元素又是一个长度为4的数组，其元素分别为当前的环境状态信息、当前环境状态下所采取的动作、策略函数的输出值以及当前环境状态下执行了根据策略选择的动作后得到的奖励值。除了动作以外，其余的数据我们在后面更新策略函数的参数的时候都会用到。

在第17行代码中，我们定义了一个变量用来累积执行动作的次数，目的是为了游戏能在有限的时间内结束。在第31行代码中，我们将这个值确定为了5000，即如果agent执行了5000次动作后，杆子还没有倒下，那么就主动结束游戏，因为这时候agent已经能够把“CartPole-v1”游戏玩得很好了。

第22行代码是将当前的环境状态以及当前的策略函数的参数带入到策略函数中，由策略来选择下一个要执行的动作。接着在第24行执行了这个动作，并在第28行更新了环境的状态信息，继续游戏。

接下来我们实现算法的主体部分，即使用梯度上升的方法优化策略函数的参数，使得agent得到的累积奖励更大：

34  def monte_carlo_policy_gradient(env):
35  # 初始化参数（学习率和折扣因子）
36      learning_rate = -0.0002
37      discount_factor = 0.95
38  
39      # 随机初始化策略函数的参数theta
40      theta = np.random.rand(4)
41  
42      # 让agent玩2000个回合
43      for i in range(2000):
44          # 生成一条完整的游戏情节：episode
45          episode = generate_an_episode(env, theta)
46  
47          # 使用梯度上升的方法优化策略函数的参数
48          for t in range(len(episode)):
49              observation, action, s, reward = episode[t]
50              # 根据蒙特卡洛策略梯度算法中的公式更新参数theta
51              theta += learning_rate * discount_factor ** t * reward *
s * (1 - s) * (-observation)
52      # 测试策略的性能
53      reward = test(env, theta)
54      print('Total reward：', reward)

首先我们初始化学习率和折扣因子，然后随机初始化了策略函数的参数。这里我们一共让agent玩了2000个回合的游戏，每一个回合的游戏都会生成一条完整的游戏情节“episode”。从第48行到第51行代码，我们利用这3000个“episode”对策略函数的参数进行优化。核心在于第51行代码，其中是策略函数对参数的导数的计算结果。

到这里，实现蒙特卡洛策略梯度算法玩“CartPole-v1”游戏的主要代码都完成了，我们想要知道实际的效果怎么样，所以在第53行我们调用了一个测试函数：

55 def test(env, theta):
56 # 重置游戏环境
57 observation = env.reset()
58 total_reward = 0.
59
60 # agent最多执行3000个动作（即奖励值达到3000后就结束游戏）
61 for i in range(3000):
62 # 可视化游戏画面（重绘一帧画面）
63 env.render()
64 # 使用策略函数选择下一个动作
65 s, action = policy_function(theta, observation)
66 # 执行动作
67 observation, reward, done, info = env.step(action)
68 # 计算累积奖励
69 total_reward += reward
70
71 if done:
72 break
73 return total_reward

最后我们定义一个程序的入口“main”函数：

74 if __name__ == "__main__":
75 # 注册游戏环境
76 game_env = gym.make('CartPole-v1')
77 # 取消限制
78 game_env = game_env.unwrapped
79 # 让agent开始学习玩“CartPole-v1”游戏
80 monte_carlo_policy_gradient(game_env)

第78行代码中“unwrapped”的目的是取消Gym中对于游戏的各种限制，例如在“CartPole-v1”游戏中，如果不加这一行代码，那么agent最多只能执行500个动作（即奖励值最高为500），超过这个值后，游戏就自动结束。

5.3 Actor Critic算法

在这一小节里我们将使用Actor Critic算法解决Gym的过山车（MountainCar）问题。

如图左所示，小车位于两座山之间，其目标是抵达右侧山峰插着黄色小旗的位置。小车的动力无法让其一次性到达目标位置，需要通过来回行驶增加动力。游戏的环境信息如图右所示，主要由小车的位置信息和速度信息两部分组成，黄色小旗在0.5的位置。在这个游戏中，我们的Agent（即小车）可以执行三个动作：施加一个向左的力，、不施加力以及施加一个向右的力。我们可以通过数值“0、1、2”来控制这三个力。

一文带你实战强化学习（下） | DQN

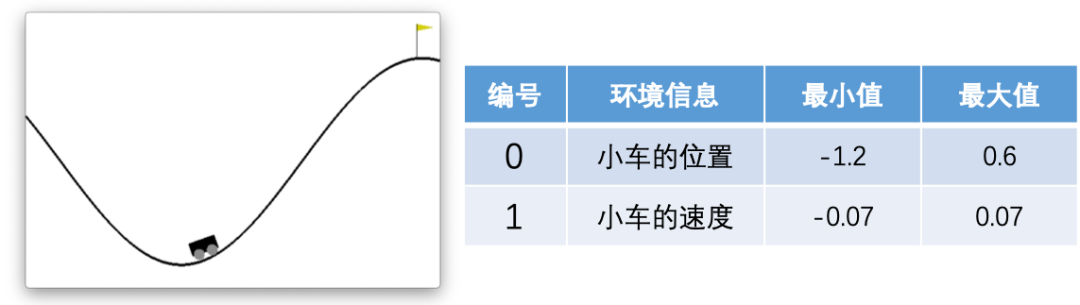
“MountainCar-v0”游戏示意图

首先我们导入需要的包：

1  import gym
2  import numpy as np
3  import random

接着实现策略函数部分：

4  def policy_function(observation, theta):
5      weight = np.dot(theta, observation)
6  
7      # 采用ε贪心（ε-greedy）搜索对环境进行探索
8      rand_num = random.random()
9      epsilon = 0.8
10      if rand_num > epsilon:
11          # 随机选择一个动作
12          s = 0
13          action = random.randint(0, 2)
14      else:
15          # 策略函数：y=[e^x-e^(-x)]/[e^x+e^(-x)]
16          s = (np.exp(weight) - np.exp(-weight)) / (np.exp(weight) + np.exp(-weight))
17          if s < -0.3:
18              action = 0  # 施加一个向左的力
19          elif s > 0.3:
20              action = 1  # 不施加力
21          else:
22              action = 2  # 施加一个向右的力
23  
24      return s, action

这里我们使用函数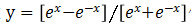一文带你实战强化学习（下） | DQN 作为策略函数，第5行代码中我们将参数与环境参数的点积作为策略函数的参数。我们使用了ε贪心搜索对环境进行探索，以0.8的概率根据当前的策略来选取动作，以0.2的概率随机选取动作。

在第17至22行代码中，由于我们的策略函数其值域为（-1,1），我们将其划分为三块，当“s”的值落在不同部分时执行不同的动作。

接下来实现actor部分：

25  def actor(env, observation, theta, pre_phi, phi, df_gamma, df_lambda):
26      # 学习率
27      alpha = 0.001
28      while True:
29          # 根据当前策略选择动作
30          s, action = policy_function(observation, theta)
31  
32          pre_observation = observation
33  
34          # 执行选择的动作并得到反馈信息（新的环境状态、奖励等）
35          observation, reward, done, info = env.step(action)
36  
37          # 可视化游戏画面（重绘一帧画面）
38          env.render()
39  
40          delta, pre_phi, phi = critic(pre_phi, phi, pre_observation, observation, reward, df_gamma, df_lambda)
41  
42          # 更新策略函数的参数 theta
43          theta += alpha * df_lambda * delta * (1 - s * s) * (-pre_observation)
44  
45          df_lambda *= df_gamma
46  
47          # 游戏结束后重置环境
48          if done:
49              observation = env.reset()

Actor和Critic部分的代码完全依照4.4节中我们给出的Actor Critic算法实现。

第30行代码中，我们根据策略选取待执行的动作，第35行代码中我们通过执行动作获取环境的反馈信息。第40行代码中，我们调用Critic函数，这里返回的delta值反映了当前动作的好坏，我们用该值来优化策略函数。第43行代码中“(1 – s * s) * (-pre_observation)”是策略函数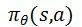一文带你实战强化学习（下） | DQN 对θ求导的结果。

50  def critic(pre_phi, phi, pre_observation, observation, reward, df_gamma, df_lambda):
51      # 学习率
52      beta = 0.001
53  
54      # 计算当前状态的价值
55      v = np.dot(phi, observation)
56      v = 1 / (1 + np.exp(-v))
57      # 计算上一状态的价值
58      pre_v = np.dot(pre_phi, pre_observation)
59      pre_v = 1 / (1 + np.exp(-pre_v))
60  
61      delta = reward + df_gamma * v - pre_v
62  
63      pre_phi = phi
64      # 更新价值函数的参数 phi
65      phi += beta * df_lambda * delta * pre_v * (1 - pre_v) * (-pre_observation)
66  
67      return delta, pre_phi, phi

第55至59行代码中，我们计算了当前状态的价值以及执行动作a之前的状态的价值。我们使用函数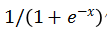一文带你实战强化学习（下） | DQN 作为状态价值函数。第61行代码中，我们用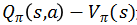来评判动作a的好坏，并用其来优化价值函数。第65行代码中，“pre_v * (1 – pre_v) * (-pre_observation)”是价值函数对参数φ的导数。

接着我们定义一个actor_critic函数：

68  def actor_critic(env):
69      observation = env.reset()
70  
71      # 随机初始化策略函数和状态价值函数的参数
72      theta = np.random.rand(2)
73      phi = np.random.rand(2)
74      pre_phi = phi
75  
76      # 折扣因子
77      df_gamma = 0.9
78      df_lambda = 1
79  
80      actor(env, observation, theta, pre_phi, phi, df_gamma, df_lambda)

在第72和73行代码中我们随机初始化了策略函数和状态价值函数的参数，因为游戏的环境由两个因素构成，因此这里参数定义为长度为2的数组。最后我们让Agent开始学习：

81 if __name__ == "__main__":
82 # 注册游戏环境 MountainCar-v0
83 game_env = gym.make('MountainCar-v0')
84 # 取消限制
85 game_env = game_env.unwrapped
86 # 开始学习玩“MountainCar-v0”游戏
87 actor_critic(game_env)

你也许还想看：

● 一文带你实战强化学习（上） | DQN

● 深度强化学习（DRL）专栏开篇

● 图像质量评估|调研

欢迎扫码关注：

一文带你实战强化学习（下） | DQN