学习率的Logistic回归结构

在这一部分中，我们将设计一个简单的算法来区分猫图像和狗图像。我们将使用神经网络思维方式建立Logistic回归模型。下图解释了为什么Logistic回归实际上是一个非常简单的神经网络(一个神经元)：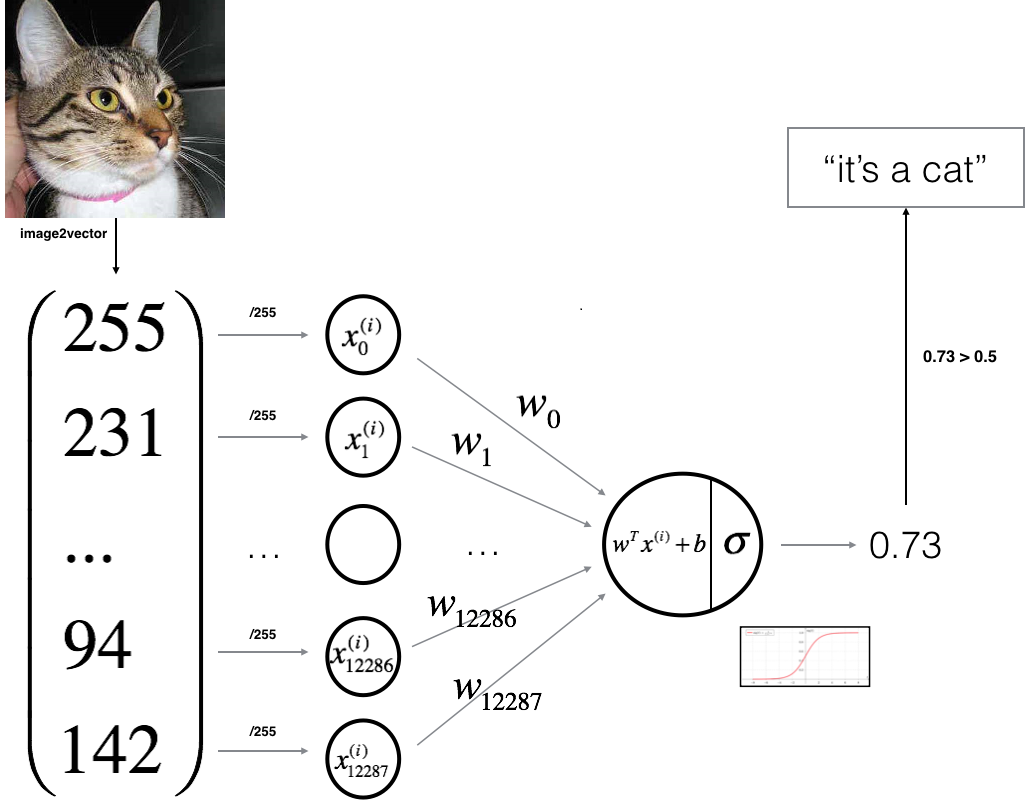

我们算法的一部分：

我们将用来构建“神经网络”的主要步骤是：

·定义模型结构(数据形状)。·初始化模型参数。·通过最小化成本了解模型参数：-计算电流损耗(前向传播)。-计算电流梯度(反向传播)。-更新参数(梯度下降)。·使用学习的参数(在测试集上)进行预测。·分析结果并结束教程。

我们将分别构建上述部分，然后将它们集成到一个名为model()的函数中。

在我们的第一部分教程中，我们已经编写了一个sigmoid函数，因此我将从那里复制它：

正向传播：

首先，权重和偏差值通过模型向前传播，以得到预测的输出。在每个神经元/节点，输入的线性组合然后乘以激活函数-在我们的例子中是Sigmoid函数。在这个过程中，权重和偏差从输入传播到输出称为前向传播。在达到预测输出后，计算训练示例的损失。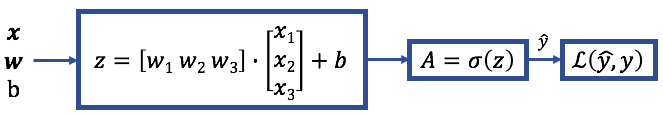

以下是一个示例的前向传播算法的数学表达式：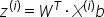

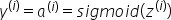
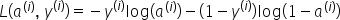
然后，通过对所有训练示例求和来计算成本：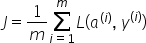

我们最终的前向传播成本函数将如下所示：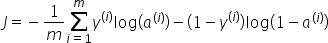

反向传播：

反向传播是计算从损失函数返回到输入的偏导数的过程。我们正在更新w和b的值，这些值使我们达到最小值。写出从da开始的偏导数会很有帮助，看看如何得到dw和db。

反向传播的数学表达式(计算导数)：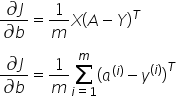

对前向和后向传播进行编码：

因此，我们将实现上面解释的函数，但首先，让我们看看输入和输出是什么：

参数：

W-权重，大小的NumPy数组(行*列*通道，1)；b-偏置，标量；X-大小的数据(行*列*通道，示例数)；Y-大小的真“标签”向量(如果是狗，则包含0；如果是猫，则包含1)；大小(1，示例数)。

返回：

Logistic回归的成本-成本；dw-损失相对于w的梯度，形状与w相同；db-损失相对于b的梯度，形状与b相同。

以下是我们在视频教程中编写的代码：

让我们用示例数据测试一下上面的函数：

因此，您应该获得：

完整教程代码：

结论：

因此，在本教程中，我们定义了通用学习体系结构，并定义了实现学习模型所需的步骤。我解释了什么是前向传播和后向传播，我们学习了如何在代码中实现它们。在下一教程中，我们将继续介绍优化算法。

最初发表于https://pylessons.com/Logistic-Regression-part5https://pylessons.com/Logistic-Regression-part5