具有一个隐含层最终模型的神经网络

因此，我们来到了最后一个教程部分，在这里我们将在nn_™()中构建最终的神经网络模型。对于我们的神经网络模型，我们将按正确的顺序使用前面的函数。

首先，我们将编写一个™函数。我将从我的逻辑回归教程中复制预测代码的一部分。Iâuro™将复制其中的部分预测代码。所以我们™将使用前向传播来预测结果。

编码预测函数：

因此，我们将实现一个预测函数，但首先，让-uro™看看它的输入和输出是什么：

参数：

PARAMETERS-EUROU“Python字典，包含参数X？EUROU”大小的数据(行*列*通道，示例数量)

返回：

Y_Forecast-uro“包含X中示例的所有预测(0/1)的NumPy数组(向量

编码nn_model()函数：

因此，我们将实现最终的模型，但是和前面一样，首先让-euro™看看它的输入和输出是什么：参数：

由NumPy形状数组(ROWS*COLS*CHANNEL，样本数)表示的X_TEST？EURO“训练集；由NumPy形状数组(向量)表示的(1，样本数)的Y_TRAIN？EURO”训练标签；由NumPy形状数组(ROWS*COLS*CHANNEL，样本数)表示的X_TEST？EURO“测试集；由形状(1，样本数)的NumPy数组(向量)表示的Y_TEST？EURO”测试标签；N_num_iterationsâuro“超参数，表示优化参数的迭代次数；Learning_rate？euro”超参数，表示Optimize()的更新规则中使用的学习率；print_ostâuro“设置为true，则每200次迭代打印一次成本。

返回：

参数-欧元“模型学习到的参数。然后可以用它们来预测。

现在是运行模型并查看其在平面数据集上的执行情况的时候了。运行以下代码，使用ğ�‘>-�隐藏单元的单个隐藏层测试您的模型.

parameters = nn_model(train_set_x, train_set_y, test_set_x, test_set_y, n_h = 10, num_iterations = 3000, learning_rate = 0.05, print_cost=True)

隐藏图层的最佳选择很重要：

在我们的Logistic回归教程中，我们比较了不同学习率的结果。与Logistic回归不同，神经网络甚至可以学习高度非线性的决策边界。这一次，我们将™将我们的模型的隐藏层计数与几个选项进行比较。运行下面的代码。您也可以随意尝试与我已初始化的值不同的值：

注意：我修改了nn_model函数，因此它可能与您在视频教程中看到的有所不同，因为在培训模型收到的错误很少之后，因此解决了这些错误，我们可以得到成本图。

我们将收到这样的训练和测试结果：Num_Iterations=2,000，™_Rate=0.1：

隐藏层为：74.20859713428857迭代后成本1400：0.586238迭代后成本1600：0.572674迭代后成本1800：0.571317训练准确率：74.20859713428857测试精度：60.31800：0.512501训练精确度：70.37654115294902测试准确率：70.37654115294902测试准确率：60.4%-欧元“-欧元”隐藏层为：100迭代后成本1400：0.561368迭代后成本1600：0.530406迭代后成本1800：0.563748训练精度：70.35988003998668欧元“-欧元”隐藏层为：2001400迭代后成本：0.596620迭代后成本1600：0.550028迭代后成本1800：0.541246训练准确率：69.86004665111629%测试精度：59.8%-欧元“-欧元”-欧元-EURO“-EURO”隐藏层是：4001400迭代后成本：0.606300迭代后成本1600：0.577356迭代后成本1800：0.572363训练准确率：71.242919026991%测试准确率：60.4%EURO“-EURO”？EURO“？EURO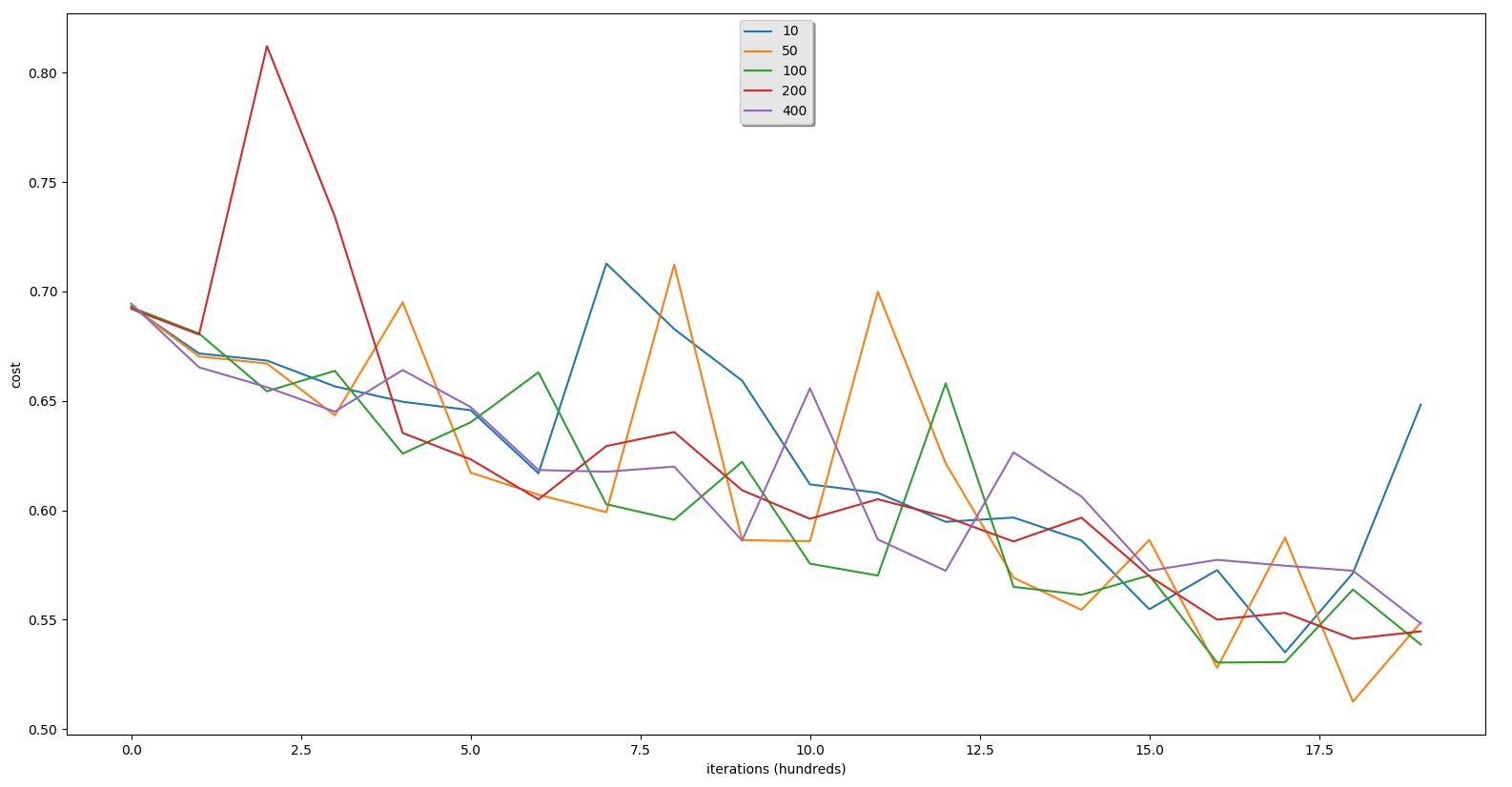

我们将收到这样的训练和测试结果：Num_™=10000，Learning_Rate=0.05：

隐藏层为：10迭代后成本9400：0.296215迭代后成本9600：0.285913迭代后成本9800：0.440895训练准确率：82.3558813728757%测试精度：60.3%-欧元“-欧元”-欧元9800：0.138445训练精度：94.65178273908697%测试精度：59.300000000000004？欧元“？欧元”？欧元？欧元“？欧元”？欧元？欧元？欧元“-欧元”隐藏层为：2009400迭代后的成本：0.113325迭代后的成本9600：0.166675迭代后的成本9800：0.133236训练准确率：89.4368543818727%测试精度：61.3%-欧元“欧元“、欧元”、欧元、欧元“欧元”、欧元“、欧元”隐藏层是：400迭代后成本9400：3.607211迭代后成本9600：0.349736迭代后成本9800：0.157746训练准确率：97.3842052649117%测试精度：62.8%、欧元？EURO“？EURO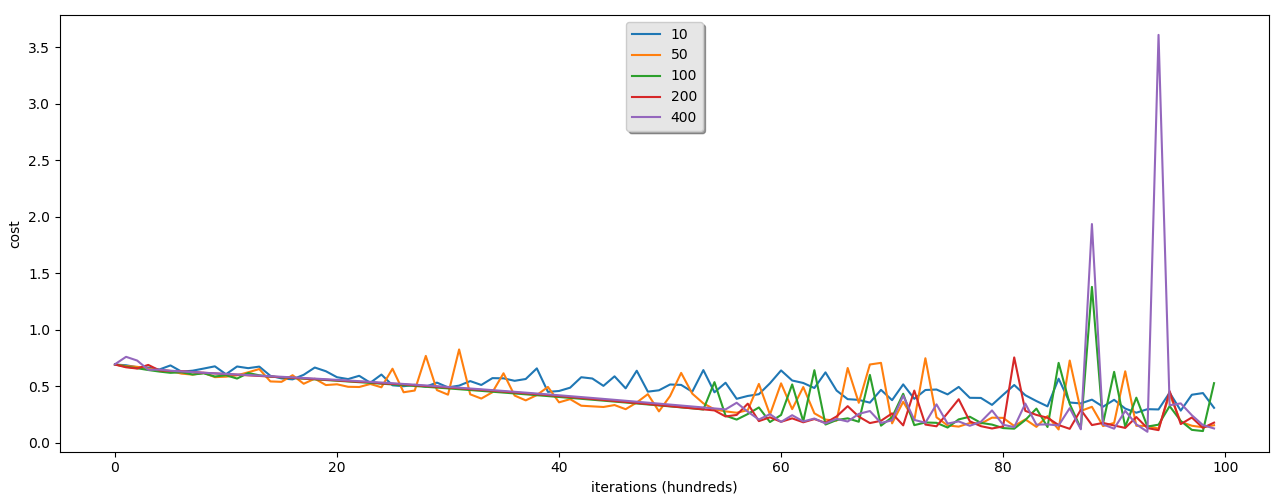

从这些图表中，您可以看到我们收到的训练准确率比测试高得多。这是因为数据过度拟合。这意味着我们的模型很难用以前™没有看到的数据来预测动物。我们不能在这里用一个隐层神经网络做得更好。™。我们将通过一个深度神经网络来看看我们™™会收到什么。

顺便说一句，你可以看到我们有400个隐含层的神经网络只比我们的Logistic回归模型好3%。It？uro™‘s没有那么令人印象深刻。我们将看看通过更深层次的网络我们能收到什么。™

我将完整的教程代码上传到同一个GitHub页面，在那里我上传了逻辑回归最终代码，因为我们使用相同的数据集。在我们完成了深度神经网络教程之后，我们将对所有这些教程的结果进行比较(™)。GitHub

结论：

所以我们最终完成了另一个关于神经网络的教程系列，只有一个隐藏层。如果您自己测试了上面的代码，您可能会说它与我们的逻辑回归代码没有太大不同。但是教我们的模型识别猫和狗需要很长的时间。与精确度相比，训练模型所需的时间是不值得的。因此，在我们的下一个教程系列中，我们将开始构建深度神经网络，并且我们将拒绝使用Sigmoid低效函数。™？™将拒绝使用Sigmoid低效函数。

要获得此模型的更多体验，您可以在不同的数据集上测试性能。具有一个隐藏层的神经网络在我们不需要从图像中识别对象的任务中可能工作得更好。(™)此外，您可以尝试调整学习速率或多次迭代。

在接下来的一步一步深入神经网络教程中见。

最初发表于https://pylessons.com/Neural-network-single-layer-part4https://pylessons.com/Neural-network-single-layer-part4