引言
这个项目是关于在给定单目图像和相应的深度图像的情况下,使用深度学习方法来估计3D空间中两个任意点之间的欧几里得距离。所提出的技术是用户友好的,要求用户在单目图像上选择两个任意点。采用自动编码器-人工神经网络结构方法,利用自动编码器网络提取特征向量,并用其建立基于人工神经网络(ANN)的回归模型。估计欧氏距离的平均偏差为0.059米。实验结果表明了该技术的重要性,该技术可以应用于各种尺寸测量应用中。下面给出的流程图描述了该方法。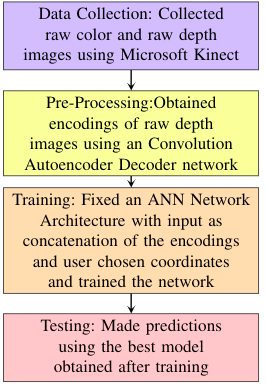
数据收集
任何机器学习项目的先决条件都是数据。使用Microsoft Kinect来准备数据集。门被用作参照物,并在其上放置了一组作为兴趣点的贴纸(图2)。在我们收集数据的三扇门上,每扇门上都贴了七张黄色贴纸。因此,总共为每扇门获得了21个不同的目标值(贴纸对)。门的颜色和深度图像是使用Kinect摄像头同时采集的,放置在任意距离。对于摄像机的一个位置,每个门可以获得6-8个不同的角度。
为了同时捕获相同分辨率的彩色和深度图像,机器人操作系统(ROS)模块与Kinect摄像头进行了接口。通过将Kinect摄像机(在1.5-4米范围内效果最好)放置在合适的位置,使得所获得的颜色和深度图像完全可以由Kinect软件来想象,就收集了三扇门中的每一扇的数据。通过保证不同门的目标值是唯一的,共获得了63个不同的目标值。共收集了99幅原始彩色图像和相应的深度图像。每幅图像还提供了21对用于距离估计的点,从而总共给出了2079幅预处理图像。2079张图像中的每一张都标有相应的尺寸。该表如下所示。Robot Operating System (ROS) module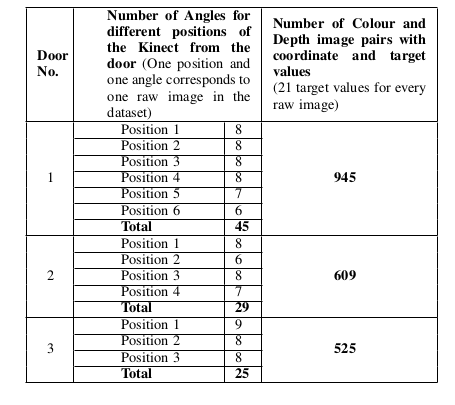
数据预处理
为了在不丢失信息的情况下从图像中提取特征,提出了一种卷积自动编码器模型。原始深度图像通过自动编码器模型,并使用编码部分的特征映射。随后将所选点的坐标与特征地图一起馈送到人工神经网络。自动编码器模型的压缩系数为4。结构如图4所示。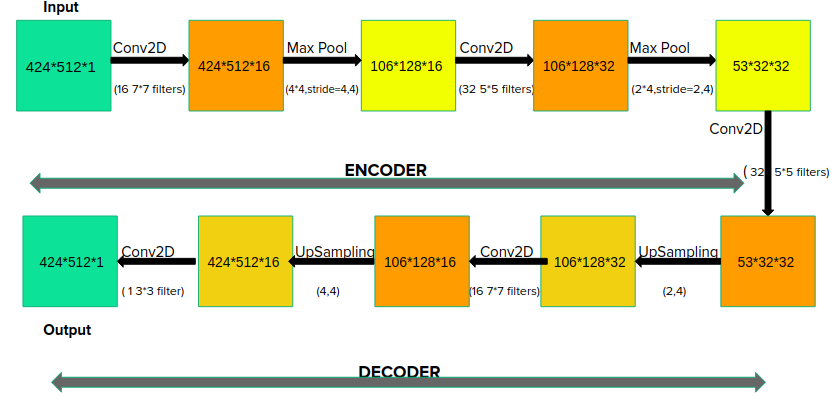
使用均方误差(MSE)损失函数和ADAM优化器。作为模型历元数函数的训练和验证损失的值可以在图5中看到。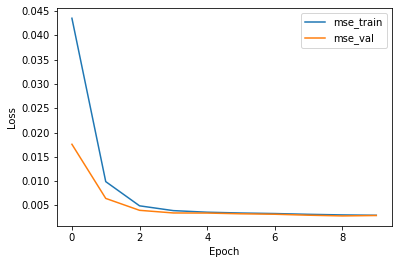
图6显示了通过模型后的原始深度图像及其相应的重建图像。
人工神经网络
从自动编码器模型(图6)的编码器部分获得的深度图像的特征图(编码)被展平。然后,将用户选择的点的坐标与平坦化的编码连接起来作为ANN的输入。输入层连接到具有1000个神经元的层,其后是批归一化层。随后一层的神经元数量减少到100个,最后输出只有一个神经元。使用MSE损失函数和RMSProp优化器。
结果
这些模型是使用带有TensorFlow后端的KERAS实现的,并在Google Colab TPU上进行了培训。模型的性能取决于预测尺寸与实际尺寸的接近程度。因为问题陈述是一个回归问题(因为输出变量可以取任何实际值),所以不能用正确预测的次数来衡量准确性,因为没有准确预测值的可能性很高。然而,模型的性能可以通过其预测的误差量来评估。例如,如果一个尺寸的真值是150厘米,那么预测148厘米或152厘米的模型比预测165厘米的模型要好。散点图如图7所示。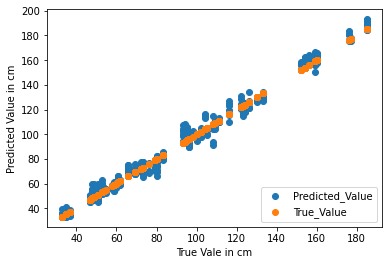
模型的均方误差为0.00339,平均误差为(+/-)0.059米。
限制
指向Github存储库的链接:https://github.com/hariharannatesh/Dimension-Estimation-from-Depth-Map-of-Monocular-Imagehttps://github.com/hariharannatesh/Dimension-Estimation-from-Depth-Map-of-Monocular-Image
原创文章,作者:fendouai,如若转载,请注明出处:https://panchuang.net/2021/07/29/%e5%9f%ba%e4%ba%8e%e5%8d%b7%e7%a7%af%e8%87%aa%e5%8a%a8%e7%bc%96%e7%a0%81%e5%99%a8%e7%9a%84%e5%8d%95%e7%9b%ae%e5%9b%be%e5%83%8f%e6%b7%b1%e5%ba%a6%e5%9b%be%e7%bb%b4%e6%95%b0%e4%bc%b0%e8%ae%a1/

