OpenCV-Python 系列 十二 | 图像的几何变换
本文是全系列中第2 / 63篇:OpenCV-Python
- OpenCV-Python 系列 四 | 视频入门
- OpenCV-Python 系列 十二 | 图像的几何变换
- OpenCV-Python 系列 二十 | 轮廓:入门
- OpenCV-Python 系列 二十八 | 直方图4:直方图反投影
- OpenCV-Python 系列 三十六 | 哈里斯角检测
- OpenCV-Python 系列 四十四 | 特征匹配 + 单应性查找对象
- OpenCV-Python 系列 五十二 | 理解K近邻
- OpenCV-Python 系列 六十 | 高动态范围
- OpenCV-Python 系列 五 | OpenCV中的绘图功能
- OpenCV-Python 系列 十三 | 图像阈值
- OpenCV-Python 系列 二十一 | 轮廓特征
- OpenCV-Python 系列 二十九 | 傅里叶变换
- OpenCV-Python 系列 三十七 | Shi-tomas拐角检测器和益于跟踪的特征
- OpenCV-Python 系列 四十五 | 如何使用背景分离方法
- OpenCV-Python 系列 五十三 | 使用OCR手写数据集运行KNN
- OpenCV-Python 系列 六十一 | 级联分类器
- OpenCV-Python 系列 六 | 鼠标作为画笔
- OpenCV-Python 系列 十四 | 图像阈值
- OpenCV-Python 系列 二十二 | 轮廓属性
- OpenCV-Python 系列 三十 | 模板匹配
- OpenCV-Python 系列 三十八 | SIFT尺度不变特征变换
- OpenCV-Python 系列 四十六 | Meanshift和Camshift
- OpenCV-Python 系列 五十四 | 理解SVM
- OpenCV-Python 系列 六十二 | 级联分类器训练
- OpenCV-Python 系列 七 | 轨迹栏作为调色板
- OpenCV-Python 系列 十五 | 图像平滑
- OpenCV-Python 系列 二十三 | 轮廓:更多属性
- OpenCV-Python 系列 三十一 | 霍夫线变换
- OpenCV-Python 系列 三十九 | SURF简介(加速的强大功能)
- OpenCV-Python 系列 四十七 | 光流
- OpenCV-Python 系列 五十五 | 使用OCR手写数据集运行SVM
- OpenCV-Python 系列 六十三 | OpenCV-Python Bindings 如何工作?
- OpenCV-Python 系列 八 | 图像的基本操作
- OpenCV-Python 系列 十六 | 形态学转换
- OpenCV-Python 系列 二十四 | 轮廓分层
- OpenCV-Python 系列 三十二 | 霍夫圈变换
- OpenCV-Python 系列 四十 | 用于角点检测的FAST算法
- OpenCV-Python 系列 四十八 | 相机校准
- OpenCV-Python 系列 五十六 | 理解K-Means聚类
- OpenCV-Python 系列 一 | 系列简介与目录
- OpenCV-Python 系列 九 | 图像上的算术运算
- OpenCV-Python 系列 十七 | 图像梯度
- OpenCV-Python 系列 二十五 | 直方图-1:查找、绘制和分析
- OpenCV-Python 系列 三十三 | 图像分割与Watershed算法
- OpenCV-Python 系列 四十一 | BRIEF(二进制的鲁棒独立基本特征)
- OpenCV-Python 系列 四十九 | 姿态估计
- OpenCV-Python 系列 五十七 | OpenCV中的K-Means聚类
- OpenCV-Python 系列 二 | 安装OpenCV-Python
- OpenCV-Python 系列 十 | 性能衡量和提升技术
- OpenCV-Python 系列 十八 | Canny边缘检测
- OpenCV-Python 系列 二十六 | 直方图-2:直方图均衡
- OpenCV-Python 系列 三十四 | 交互式前景提取使用GrabCut算法
- OpenCV-Python 系列 四十二 | ORB(面向快速和旋转的BRIEF)
- OpenCV-Python 系列 五十 | 对极几何
- OpenCV-Python 系列 五十八 | 图像去噪
- OpenCV-Python 系列 三 | 图像入门
- OpenCV-Python 系列 十一 | 改变颜色空间
- OpenCV-Python 系列 十九 | 图像金字塔
- OpenCV-Python 系列 二十七 | 直方图-3:二维直方图
- OpenCV-Python 系列 三十五 | 理解特征
- OpenCV-Python 系列 四十三 | 特征匹配
- OpenCV-Python 系列 五十一 | 立体图像的深度图
- OpenCV-Python 系列 五十九 | 图像修补
目标
- 学习将不同的几何变换应用到图像上,如平移、旋转、仿射变换等。
- 你会看到这些函数: cv.getPerspectiveTransform
变换
OpenCV提供了两个转换函数cv.warpAffine和cv.warpPerspective,您可以使用它们进行各种转换。cv.warpAffine采用2×3转换矩阵,而cv.warpPerspective采用3×3转换矩阵作为输入。
缩放
缩放只是调整图像的大小。为此,OpenCV带有一个函数cv.resize()。图像的大小可以手动指定,也可以指定缩放比例。也可使用不同的插值方法。首选的插值方法是cv.INTER_AREA用于缩小,cv.INTER_CUBIC(慢)和cv.INTER_LINEAR用于缩放。默认情况下,出于所有调整大小的目的,使用的插值方法为cv.INTER_LINEAR。您可以使用以下方法调整输入图像的大小:
import numpy as np
import cv2 as cv
img = cv.imread('messi5.jpg')
res = cv.resize(img,None,fx=2, fy=2, interpolation = cv.INTER_CUBIC)
#或者
height, width = img.shape[:2]
res = cv.resize(img,(2*width, 2*height), interpolation = cv.INTER_CUBIC)
平移
平移是物体位置的移动。如果您知道在(x,y)方向上的位移,则将其设为($t_x$,$t_y$),你可以创建转换矩阵$mathbf{M}$,如下所示:
$$ M = begin{bmatrix} 1 & 0 & t_x 0 & 1 & t_y end{bmatrix} $$
您可以将其放入np.float32类型的Numpy数组中,并将其传递给cv.warpAffine函数。参见下面偏移为(100, 50)的示例:
import numpy as np
import cv2 as cv
img = cv.imread('messi5.jpg',0)
rows,cols = img.shape
M = np.float32([[1,0,100],[0,1,50]])
dst = cv.warpAffine(img,M,(cols,rows))
cv.imshow('img',dst)
cv.waitKey(0)
cv.destroyAllWindows()
警告
cv.warpAffine函数的第三个参数是输出图像的大小,其形式应为(width,height)。记住width =列数,height =行数。
你将看到下面的结果:

旋转
图像旋转角度为$θ$是通过以下形式的变换矩阵实现的:
$$
M = begin{bmatrix} costheta & -sintheta sintheta & costheta end{bmatrix}
$$
但是OpenCV提供了可缩放的旋转以及可调整的旋转中心,因此您可以在自己喜欢的任何位置旋转。修改后的变换矩阵为
$$
begin{bmatrix} alpha & beta & (1- alpha ) cdot center.x – beta cdot center.y – beta & alpha & beta cdot center.x + (1- alpha ) cdot center.y end{bmatrix}
$$
其中:
$$
begin{array}{l} alpha = scale cdot cos theta , beta = scale cdot sin theta end{array}
$$
为了找到此转换矩阵,OpenCV提供了一个函数cv.getRotationMatrix2D。请检查以下示例,该示例将图像相对于中心旋转90度而没有任何缩放比例。
img = cv.imread('messi5.jpg',0)
rows,cols = img.shape
# cols-1 和 rows-1 是坐标限制
M = cv.getRotationMatrix2D(((cols-1)/2.0,(rows-1)/2.0),90,1)
dst = cv.warpAffine(img,M,(cols,rows))
查看结果:

仿射变换
在仿射变换中,原始图像中的所有平行线在输出图像中仍将平行。为了找到变换矩阵,我们需要输入图像中的三个点及其在输出图像中的对应位置。然后cv.getAffineTransform将创建一个2×3矩阵,该矩阵将传递给cv.warpAffine。
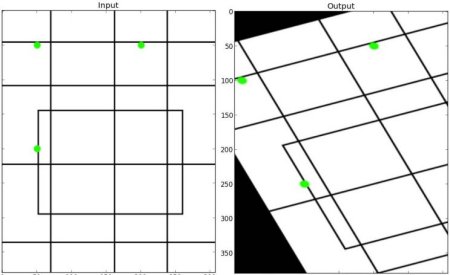
查看以下示例,并查看我选择的点(以绿色标记):
img = cv.imread('drawing.png')
rows,cols,ch = img.shape
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[10,100],[200,50],[100,250]])
M = cv.getAffineTransform(pts1,pts2)
dst = cv.warpAffine(img,M,(cols,rows))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
查看结果:
透视变换
对于透视变换,您需要3×3变换矩阵。即使在转换后,直线也将保持直线。要找到此变换矩阵,您需要在输入图像上有4个点,在输出图像上需要相应的点。在这四个点中,其中三个不应共线。然后可以通过函数cv.getPerspectiveTransform找到变换矩阵。然后将cv.warpPerspective应用于此3×3转换矩阵。
请参见下面的代码:
img = cv.imread('sudoku.png')
rows,cols,ch = img.shape
pts1 = np.float32([[56,65],[368,52],[28,387],[389,390]])
pts2 = np.float32([[0,0],[300,0],[0,300],[300,300]])
M = cv.getPerspectiveTransform(pts1,pts2)
dst = cv.warpPerspective(img,M,(300,300))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()
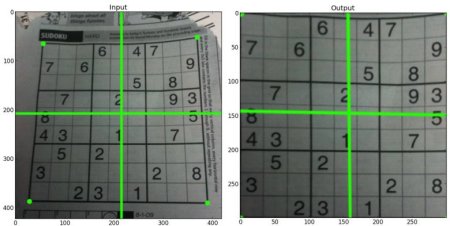
结果:
其他资源
- “Computer Vision: Algorithms and Applications”, Richard Szeliski
练习题
原创文章,作者:磐石,如若转载,请注明出处:https://panchuang.net/2020/02/28/opencv-python-%e7%b3%bb%e5%88%97-%e5%8d%81%e4%ba%8c-%e5%9b%be%e5%83%8f%e7%9a%84%e5%87%a0%e4%bd%95%e5%8f%98%e6%8d%a2/

