Logistic回归中学习率的最佳选择

要让梯度下降发挥作用，我们必须明智地选择学习率。学习率α决定我们更新参数的速度。如果学习率太大，我们可能会“超调”最优值。类似地，如果它太小，我们将需要太多迭代才能收敛到最佳值。这就是为什么使用一个良好的学习速率是至关重要的。因此，我们将比较我们模型的学习曲线和几种学习速率的选择。运行下面的代码。您也可以随意尝试与我初始化的值不同的值。GitHub链接到完整代码。GitHub link to full code.

我们将以不同的学习率接受这样的训练和测试精度：

学习率为：63.628790403198934训练准确率：63.628790403198934%测试准确率：59.0%-学习率为：0.002训练准确率：66.27790736421193%测试准确率：60.0%-学习率：0.003训练准确率：68.24391869376875%测试准确率：58.6%-学习率：0.005训练准确度：54.08197267577474%测试准确率：53.0%-学习率为：0.01训练准确率：54.18193935354882%测试准确率：53.3%

学习速度的结果可以在下面的图表中看到：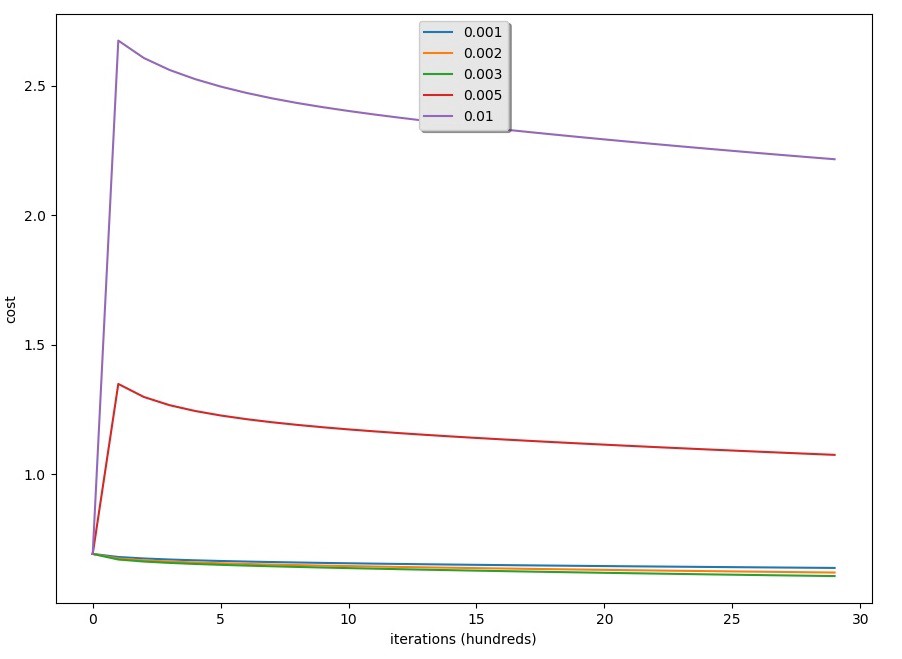

结果：

• 不同的学习率会给出不同的成本和不同的预测结果；
• 如果学习率太大(0.01)，成本可能会上下振荡。使用0.01最终仍然是一个很好的成本价值。
• 更低的成本并不意味着更好的模式。你得检查一下有没有可能是不是太合身了。当训练精度远高于测试精度时，就会发生这种情况；
• 在深度学习中，通常建议选择代价函数最小的学习率。

本Logistic回归系列教程需要记住的内容：

结论：

最后，我们用神经网络思维建立了最简单的Logistic回归模型。如果您想用它测试更多，您可以尝试学习速度和迭代次数。您可以尝试不同的初始化方法并比较结果。这是Logistic回归的最后一个系列教程。接下来，我们将开始构建一个简单的神经网络！

最初发表于https://pylessons.com/Logistic-Regression-part9https://pylessons.com/Logistic-Regression-part9