强化学习的基本迭代方法

作者|Nathan Lambert
编译|VK
来源|Towards Data Science

研究价值迭代和策略迭代。

本文着重于对基本的MDP进行理解(在此进行简要回顾)，将其应用于基本的强化学习方法。我将重点介绍的方法是"价值迭代"和"策略迭代"。这两种方法是Q值迭代的基础，它直接导致Q-Learning。

你可以阅读我之前的一些文章(有意独立)：

1. 什么是马尔可夫决策过程?(https://towardsdatascience.com/what-is-a-markov-decision-process-anyways-bdab65fd310c)
2. 强化学习的线性代数(https://towardsdatascience.com/the-hidden-linear-algebra-of-reinforcement-learning-406efdf066a)

Q-Learning开启了我们所处的深度强化学习的浪潮，是强化学习学生学习策略的重要一环。

回顾马尔可夫决策过程

马尔可夫决策过程(MDPs)是支持强化学习(RL)的随机模型。如果你熟悉，你可以跳过这一部分，不过我增加了一些相关的解释。

定义

• 状态集$s\in S，动作集$a\in A$。状态和动作是代理程序所有可能的位置和动作的集合。在高级强化学习中，状态和动作是连续，所以这需要重新考虑我们的算法。

• 转换函数T(s，a，s’)。给定当前位置和给定动作，T决定下一个状态出现的频率。在强化学习中，我们不访问这个函数，因此这些方法试图对采样数据进行近似或隐式学习。

• 奖励函数R(s，a，s’)。此函数说明每个步骤可获得多少奖励。在强化学习中，我们不使用此函数，因此我们从采样值r中学习，采样值r使算法探索环境，然后利用最优轨迹。

• 折扣因子γ(伽马，范围[0,1])可将下一步的值调整为将来的奖励。在强化学习中，我们不使用此函数，γ(gamma)控制了大部分学习算法和Bellman系优化的收敛性。

• 初始状态s0，也可能是结束状态。

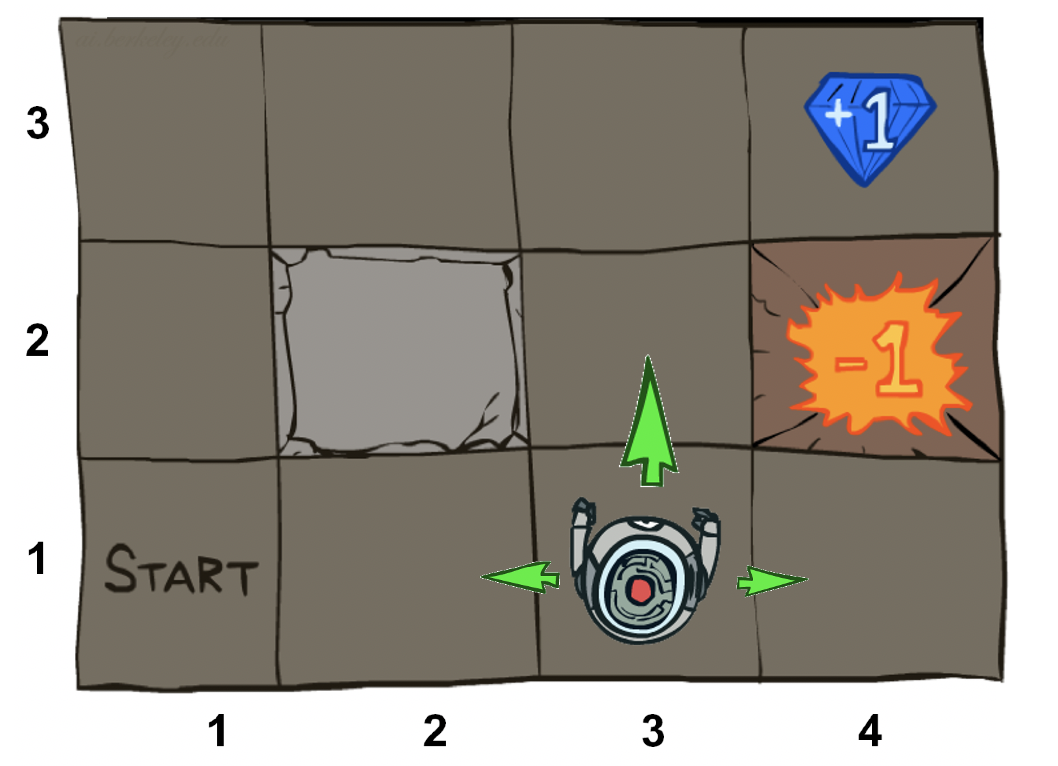
重要价值

MDP有两个重要的特征，状态值和机会节点(chance node)的q值。任何MDP或RL值中的*表示最佳数量。

• 状态值：状态的值就是从状态开始后奖励的最优递归和。

• 状态的Q值，动作对：Q值是与状态-动作对相关联的折扣奖励的最优和。

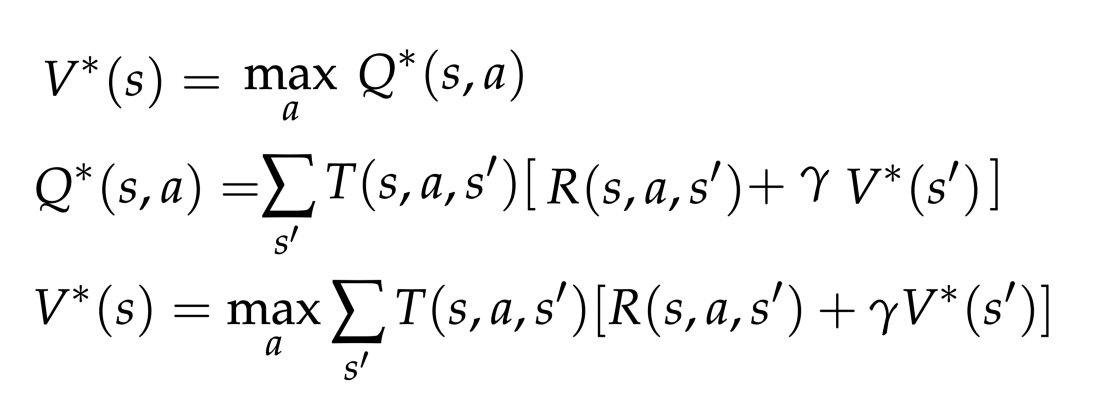
最佳值与最佳动作条件q值相关。然后，值和q值更新规则非常相似(加权转换，奖励和折扣因子)。顶部:值与q值的耦合；中部：Q值递归：，底部：值的迭代。参考：https://inst.eecs.berkeley.edu/~cs188/sp20/

引领强化学习

值迭代

学习所有状态的值，然后我们可以根据梯度来操作。值迭代直接从Bellman更新中学习状态的值。在某些非限制性条件下，Bellman更新被保证收敛到最优值。

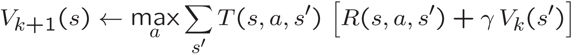
学习一项策略可能比学习一种价值观更直接。学习一个值可能需要无限长的时间来收敛到一个64位浮点数的数值精度(考虑在每次迭代中一个常数的移动平均，在开始估计为0之后，它将永远添加一个越来越小的非零数)。

策略迭代

学习与值相关的策略。策略学习增量地查看当前值并提取策略。由于动作空间是有限的，我们希望它能比值迭代收敛得更快。从概念上讲，对操作的最后一次更改将发生在小的滚动平均更新结束之前。策略迭代有两个步骤。

第一个称为策略提取，就是如何从一个值转换到一个策略，这策略使期望值最大化。

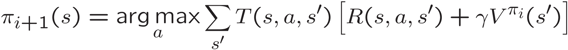
第二步是策略评估。策略评估采用策略，并以策略为条件进行值迭代。这些样本永远与策略相关，但是我们必须运行迭代算法，以减少提取相关动作信息的步骤。

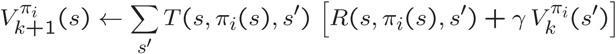
与值迭代一样，由于底层的Bellman更新，对于大多数合理的MDPs，策略迭代保证收敛。

Q值迭代

学习最优值的问题是很难从中提取出策略。argmax算子明显是非线性的，很难进行优化，因此q值迭代法向直接策略提取迈出了一步。每个状态下的最优策略就是那个状态下的最大q值。

大多数指令以"值迭代"开头的原因是，它自然地进入了Bellman更新中。Q值迭代需要一起替换两个关键MDP值关系。这样做之后，这是我们将要了解的Q-Learning的第一步。

大多数指令以值迭代开始的原因是，它可以更自然地插入Bellman更新。Q值迭代需要一起替换两个关键的MDP值关系。这样做之后，它就离我们将要了解的Q-learning一步之遥了。

这些迭代算法是怎么回事？

让我们确保你理解了所有的术语。本质上，每个更新由求和后的两个项组成(也可能是由max来进行的选择动作)。让我们用括号括起来然后讨论它们与MDP的关系。

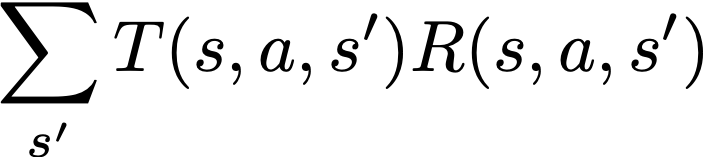
第一项是T(s，a，s’)R(s，a，s’)乘积的总和。这一项表示潜在的值和给定状态和转换的可能性。T，或者说转换，决定了从转换中获得给定回报的可能性(回想一下，一个元组s,a,s ‘决定了其中一个动作a将一个代理从一个状态s带到另一个状态s’)。这将做一些事情，这会做一些事情，例如权衡具有高奖励的低概率状态与权重较低的频繁状态。

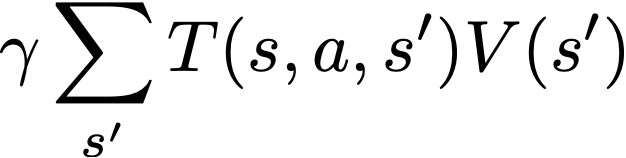
下一项决定了这些算法的“bellman特性”。它是迭代算法V的最后一步的数据加权，上面的公式有一项。这从邻近状态获取关于值的信息，这样我们就可以理解长期的转变。将这一项看作递归更新的主要发生位置，而第一项则是由环境决定的优先权重。

收敛条件

告知所有迭代算法"在某些条件下收敛到最佳值或策略"。这些条件是：

1. 状态空间总覆盖率。条件是所有状态、动作、next_state元组都是在条件策略下到达的。如果不这样做，来自MDP的一些信息将会丢失，并且值可能会停留在初始值上。

2. 折扣因子γ < 1。否则造成无限循环，并且最后趋于无穷大。

值得庆幸的是，在实践中，这些条件很容易满足。大多数探索都具有epsilon贪婪性，包括总有随机动作的机会(因此任何动作都是可行的)，并且non-one折现因子会导致更佳的性能。最终，这些算法可以在很多设置下工作，因此绝对值得一试。

强化学习

我们如何将我们所看到的变成强化学习问题？我们需要使用样本，而不是真正的T(s，a，s’)和R(s，a，s’)函数。

基于样本的学习-如何解决隐藏的MDP

MDPs中的迭代方法与解决强化学习问题的基本方法之间的惟一区别是，RL样本来自MDP的底层转换和奖励函数，而不是将其包含在更新规则中。有两件事我们需要更新，替换T(s,a,s ‘)和替换R(s,a,s ‘)

首先，让我们将转换函数近似为每个观察元组的平均动作条件转换。我们没有看到的所有值都是用随机值初始化的。这是基于模型的强化学习最简单的形式(我的研究领域)。

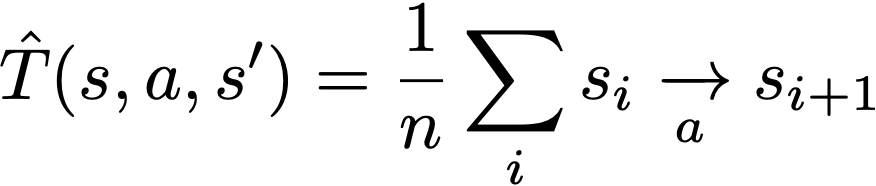
现在，剩下的就是记住如何使用奖励。但是，我们实际上每一步都有一个奖励，所以我们可以不受惩罚(方法用许多样本平均出正确的值)。考虑用采样奖励近似q值迭代方程，如下所示。

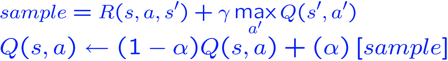
上面的等式是Q-Learning。我们从一些填充有随机值的向量Q(s，a)开始，然后收集与世界的交互并调整alpha。Alpha是一种学习率，因此当我们认为算法正在收敛时，我们将降低它。

结果表明，Q-learning与Q-value迭代非常相似，但我们只是在一个不完整的世界观下运行这个算法。

机器人和游戏中使用的Q-learning是在更复杂的特征空间中，神经网络近似于一个包含所有状态-动作对的大表格。

原文链接：https://towardsdatascience.com/fundamental-iterative-methods-of-reinforcement-learning-df8ff078652a

欢迎关注磐创AI博客站：
http://panchuang.net/

sklearn机器学习中文官方文档：
http://sklearn123.com/

欢迎关注磐创博客资源汇总站：
http://docs.panchuang.net/