什么是张量器？

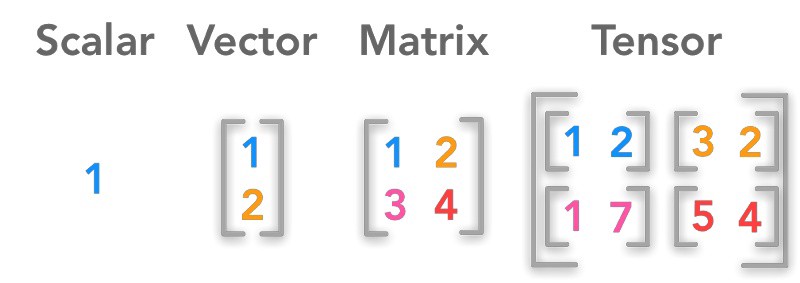
张量是机器学习系统使用的数据结构，识别张量是您应该事先掌握的一项重要技能。张量是数值数据的容器。这就是我们存储将在系统中使用的信息的方式。

有三个属性定义张量：

• 范围
• 形状
• dType：这里张量的秩是指张量的轴数。

示例：

• 矩阵的秩为2，因为它有两个轴。
• 向量的秩为1，因为它只有一个轴。

张量的形状是指沿每个轴的维数。例如：

• 方阵可以有维数(2，2)。
• 级别3张量(3、5、8)可以有维度。

张量的数据类型是指它包含的数据类型。一些受支持的数据类型包括：

• 浮动32
• Float64
• uint8
• int32
• int64

标量(0D张量)的阶数为0，并且包含单个数字。这些称为0维张量。下图显示了如何使用NumPy创建0维张量。

import numpy as np
tensor = np.array(42)

向量(一维张量)具有一阶，表示一系列数字。下图显示了一个形状为(4，)的向量。

import numpy as np
tensor = np.array([8, 16, 32, 64])

矩阵(2D张量)有第二行，表示向量数组。矩阵的两个轴通常称为行和列。下图显示了一个形状为(3，4)的矩阵。

import numpy as np
tensor = np.array([[2, 10, 20, 22],
                   [8, 16, 32, 64],
                   [5, 10, 15, 20]])

您可以通过将低维张量打包到数组中来获得高维张量(3D、4D等)。例如，将一个4D张量打包到一个数组中就可以得到一个8D张量。

以下是一些常见的张量表示法：

• 矢量：1D-(特性)
• 序列：2D-(切片，属性)
• 图像：3D-(高度、宽度、通道)
• 视频：4D-(帧、高、宽、通道)

通常，机器学习算法一次处理数据的子集，称为批处理。

使用数据集时，张量的第一个轴保留为批量大小(样本数)。

例如，如果您正在处理2D张量(矩阵)，则一个组总共将有3个维度：

白色小方块(样本、行、列)

请注意，第一个轴是我们组中的矩阵数量。

遵循相同的逻辑，一组图像可以表示为4D张量：

• 白色小正方形(示例、高度、宽度、通道)
• 白色小方块(样本、帧、高度、宽度、通道)