Logistic回归成本优化函数

让我们从我们在上一个教程中定义的步骤开始，以及剩下要做的事情：

·定义模型结构(数据形状)(完成)；·初始化模型参数；·通过将成本降至最低来了解模型的参数：-计算电流损耗(正向传播)(完成)；-计算电流梯度(反向传播)(完成)；-更新参数(梯度下降)；·使用学习到的参数进行预测(在测试集上)；·分析结果并总结本教程。

在上一个教程中，我们定义了模型结构，学习了计算成本函数及其梯度。在本教程中，我们将编写一个优化函数来使用梯度下降来更新参数。

因此，我们将编写通过最小化成本函数J来学习w和b的优化函数。对于参数θ，更新规则是(α是学习率)：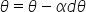

Logistic回归中的成本函数：

我们使用成本函数进行Logistic回归的原因之一是它是一个凸函数，只有一个全局最优解。你可以想象把一个球滚下碗状的功能(如下图所示)–它会落在底部。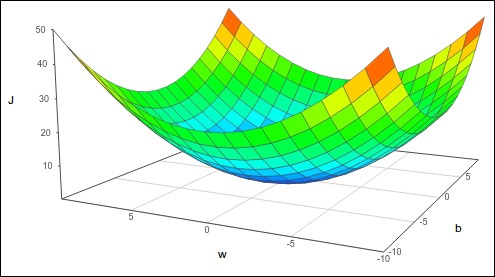

同样，要找到最小成本函数，我们需要找到最低点。要做到这一点，我们可以从函数的任何位置开始，沿着最陡峭的坡度方向迭代向下移动，调整w和b的值，使我们达到最小值。为此，我们使用以下两个公式：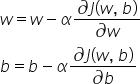

在这两个方程中，偏导数dw和db分别表示w和b的变化对成本函数的影响。通过找到坡度并取该坡度的负值，我们确保我们将始终朝着最小的方向移动。为了更好地理解，让我们以图形方式查看dw：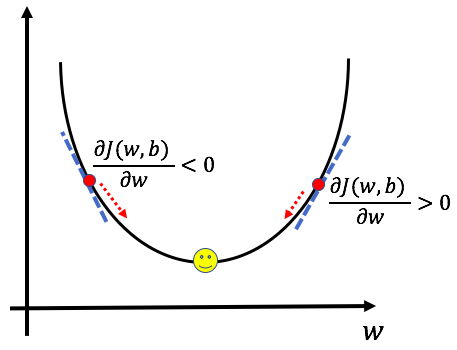

当导数项为正时，我们朝相反的方向移动，朝向w的减小值。当导数为负数时，我们朝向增加w的方向移动，从而确保我们总是朝向最小值移动。

偏导数前面的阿尔法项称为学习率，它衡量每次迭代要迈出多大的一步。学习参数的选择是一个很重要的问题-太小，模型需要很长时间才能找到最小值，太大，模型可能会超过最小值而找不到最小值。

梯度下降是学习过程的本质-通过它，机器学习权重和偏差的值是什么使成本函数最小化。它通过迭代地将其对一组数据的预测输出与训练过程中的真实输出进行比较来做到这一点。

编码优化功能：

因此，我们将实现一个优化函数，但首先，让我们看看它的输入和输出是什么：

参数：

W-权重，大小的NumPy数组(ROWS*COLS*CHANNEWS，1)；b-BIAS，标量；X-大小的数据(ROWS*COLS*CHANCES，示例数)；Y-真“标签”向量(如果是狗，则包含0；如果是猫，则包含1)；Num_Iterations-优化循环的迭代次数；Learning_Rate-梯度下降更新规则的学习率；Print_Cost-True，用于每100步打印损失。

返回：

参数-包含权重w和偏差b的字典；梯度-包含关于成本函数的权重和偏差的梯度的字典；成本-在优化期间计算的所有成本的列表。

以下是代码：

让我们用编写propogate()函数的上一个教程中的变量来测试上面的函数：

如果结果是一切正常，您应该得到：

完整教程代码：

因此，在本教程中，我们学习了如何更新学习参数(梯度下降)。您看到了我们如何使用来自前向和后向传播的参数来教导我们的模型。在下一个教程中，我们将编写一个函数来计算预测。

最初发表于https://pylessons.com/Logistic-Regression-part6https://pylessons.com/Logistic-Regression-part6