成本函数:
至此,我们已经初始化了深度参数并编写了前向传播模块。现在我们将实现代价函数和反向传播模块。与前面一样,我们需要计算成本,因为我们想检查我们的模型是否真正在学习。要计算交叉熵成本J,我们将使用前面已经看到的公式: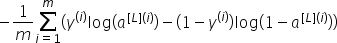
COMPUTE_COST函数的代码:
参数:
Al-与标签预测对应的概率向量,Shape(1,示例数)。Y-true“label”向量(例如:如果是狗,则包含0,如果是猫,则包含1)、Shape(1,示例数)。
返回:
成本-交叉熵成本。
这只是一行代码,所以我们不会测试它,因为它在我之前的教程中已经测试过了。
反向传播函数:
就像前向传播一样,我们将实现反向传播的帮助器函数。我们知道,传播是用来计算参数的损失函数的梯度的。我们需要写出线性->Relu->线性->Sigmoid模型的前向和后向传播。这将如下所示: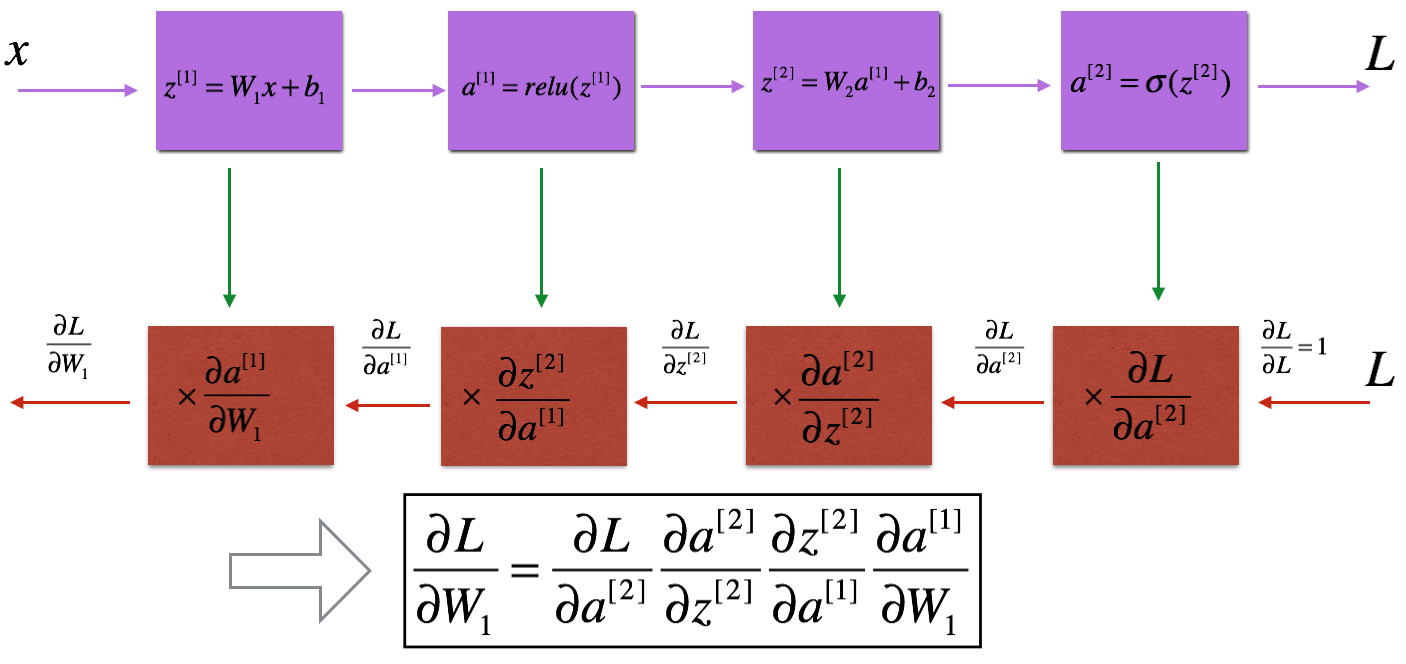
与前向传播类似,我们将分三步构建后向传播:
- 线性向后;
- 线性->反向激活,其中激活计算RELU或S型激活的导数;
- [线性->重排]×(L-1)->线性->向后S型(整个模型)
线性向后:
对于层l,线性部分为: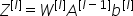
我想我们已经计算过导数了:
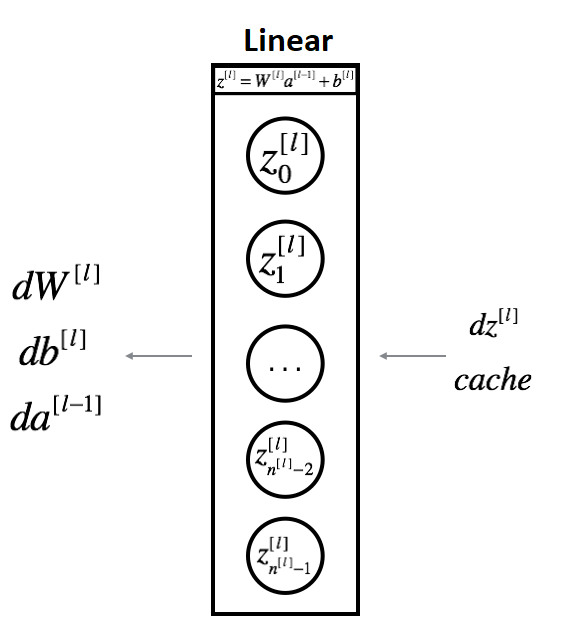
将使用输入DZ[l]计算三个输出(dw[l]、db[l]、da[l])。以下是我们的两层神经网络教程系列中需要的公式: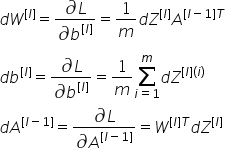
我们的LINEAR_BACKWARD函数的代码:
参数:
dz-与(当前层l的)线性输出相关的成本梯度;来自当前层中前向传播的值的缓存元组(A_prev,W,b)。
返回:
DA_PREV-关于(前一层l-1的)激活的成本梯度,形状与A_PREV相同;DW-成本到W(当前层l)的梯度,形状与W相同;DB-成本到b(当前层l)的梯度,形状与b相同。
线性-激活反向功能:
接下来,我们将创建一个合并两个助手函数的函数:LINEAR_BACKBACK和激活LINEAR_ACTIVATION_BACKBACK的BACKUP步骤。
为了实现LINEAR_ACTIVATION_BACKUP,我们将编写两个反向函数:
- Sigmoid_Backward:Sigmoid单元的反向传播:
- RELU_BACKED:RELU单位的反向传播(_B):
如果g(.)是激活函数,sigmoid_back和relu_back计算: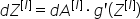
LINEAR_ACTIVATION_BACKUP函数的代码:
参数:
DA-当前层l的激活后梯度;缓存-我们存储的用于有效计算反向传播的值的元组(LINEAR_CACHE,ACTIVATION_CACHE);激活-要在该层中使用的激活,存储为文本字符串:“Sigmoid”或“relu”。
返回:
da_prev-激活成本的梯度(前一层l-1),形状与A_prev相同;dw-成本至W(当前层l)的梯度,形状与W相同;db-成本至b(当前层l)的梯度,形状与b相同。
完整教程代码:
本教程花了一些时间。我将在下一个教程中完成我们的向后功能。在下一个教程中,我们将编写向后的最终模块和函数来更新参数。在那之后,我们将最终训练我们的模型。
最初发表于https://pylessons.com/Deep-neural-networks-part3https://pylessons.com/Deep-neural-networks-part3
原创文章,作者:fendouai,如若转载,请注明出处:https://panchuang.net/2021/07/27/%e6%b7%b1%e5%ba%a6%e7%a5%9e%e7%bb%8f%e7%bd%91%e7%bb%9c%e5%8f%8d%e5%90%91%e4%bc%a0%e6%92%ad/

