感知机：教程，实现和可视示例

作者|Dorian Lazar
编译|VK
来源|Towards Data Science

感知器是人工神经网络的组成部分，它是大脑中生物神经元的简化模型。感知器是最简单的神经网络，仅由一个神经元组成。感知器算法由Frank Rosenblatt于1958年发明。

以下是生物神经元的图示：

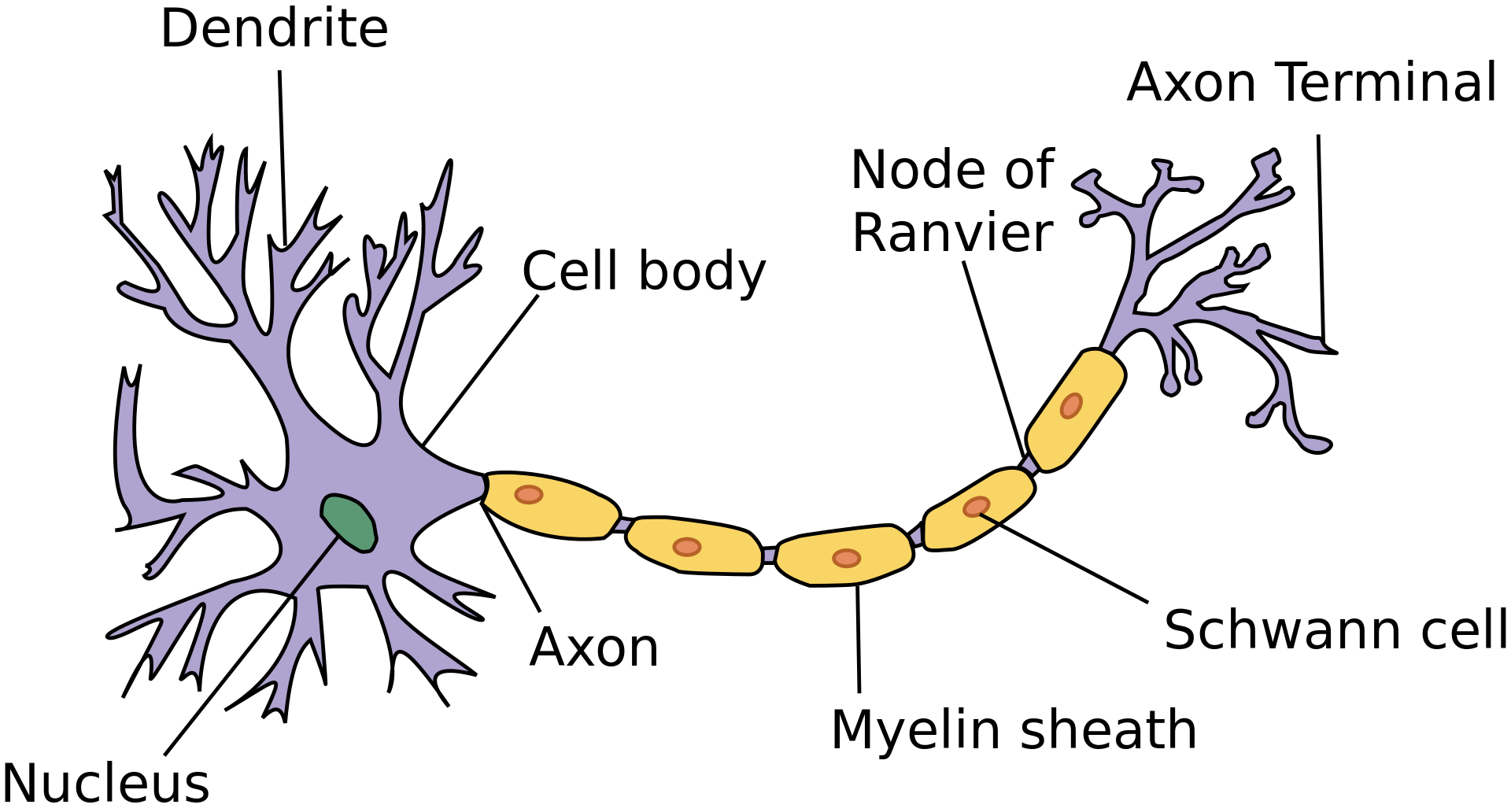
经由树突接收到神经元的大部分输入信号。其他神经元与这些树突形成约1,000至10,000个连接。来自连接的信号称为突触，通过树突传播到细胞体内。细胞体内的电位增加，一旦达到阈值，神经元就会沿着轴突发出一个尖峰，该轴突通过轴突末端连接到大约100个其他神经元。

感知器是真实神经元的简化模型，它尝试通过以下过程来模仿它：接收输入信号，将它们称为x1，x2，…，xn，计算这些输入的加权和z，然后将其传递阈值函数ϕ并输出结果。

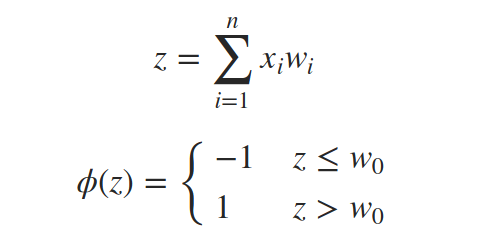
但将w0作为阈值和将w0作为偏置添加到和中并将阈值改为0是一样的。我们考虑一个始终设置为1的附加输入信号x0。

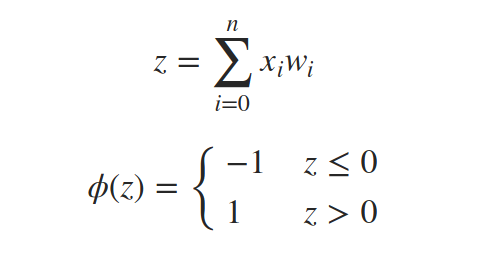
下面是一个感知器：

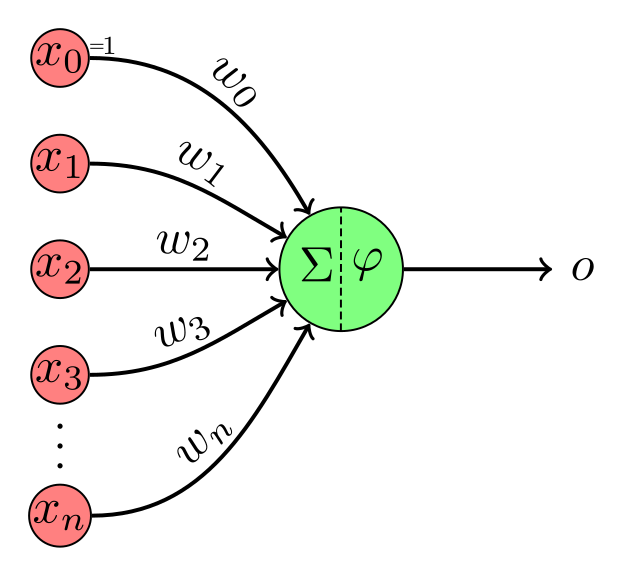
要使用向量表示法，我们可以将所有输入x0、x1、…、xn和所有权重w0、w1、…、wn放入向量x和w中，当它们的点积为正时输出1，否则输出-1。

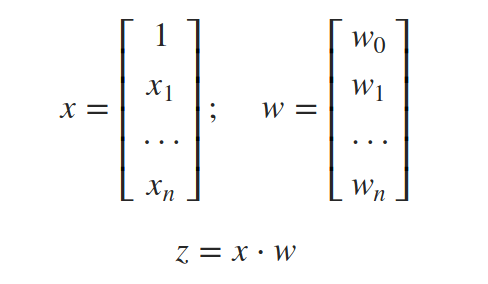
以下是仅使用2个输入x1和x2的几何表示，以便我们可以在2维中绘制：

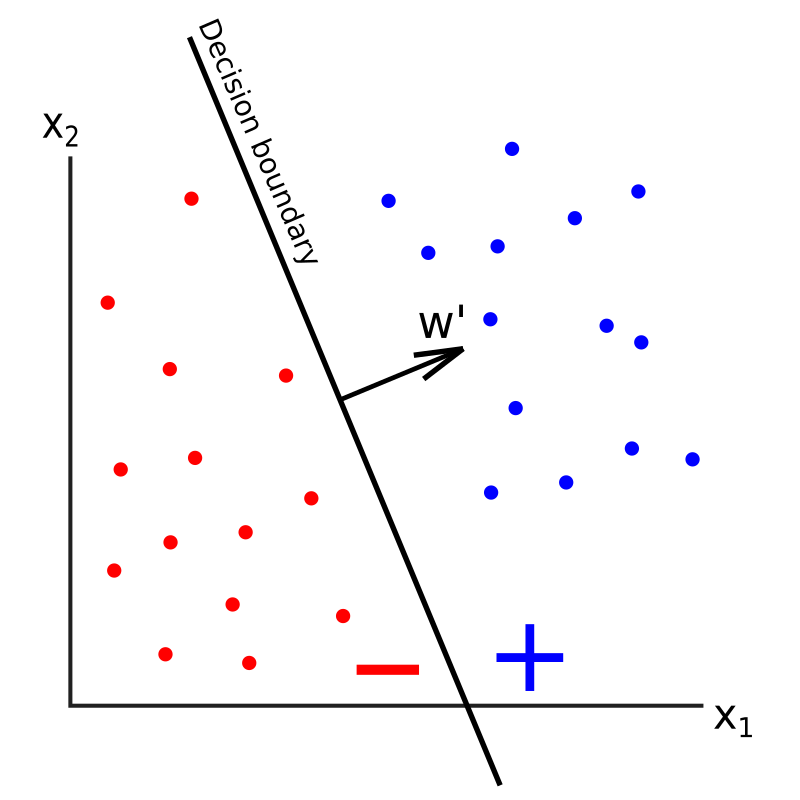
如上所示，具有2个输入的感知器的决策边界是一条直线。如果有3个输入，则决策边界为二维平面。一般来说，如果我们有n个输入，决策边界将是一个称为n-1维的超平面，该超平面将我们的n维特征空间分成两部分：一部分是将点分类为正的，另一部分是将点分类为负的(按照惯例，我们将认为恰好在决策边界上的点是负的)。因此，感知器是一个二元分类器，其权值是线性的。

在上面的图像中，w’表示没有偏移项w0的权重向量。w’垂直于决策边界并指向正分类点的性质。该向量决定了决策边界的斜率，而偏移项w0决定了决策边界沿w’轴的偏移。

到目前为止，我们讨论了感知器如何根据输入信号及其权值做出决策。但是，感知者实际上是如何学习的呢？如何找到合适的参数w0，w1，…，wn，以便进行良好的分类？

感知器算法是基于以下简单更新规则的迭代算法：

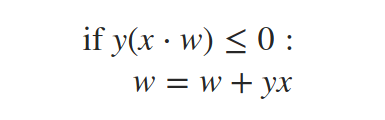
其中y是当前数据点x的标签(要么-1要么+1)，w是权重向量。

我们的更新规则怎么说？点积x⋅w只是感知器基于当前权重的预测(其符号与预测标签的符号相同)。表达式y(x⋅w)只能小于或等于0，前提是实际标签y不同于预测标签φ(x⋅w)。因此，如果真标签和预测标签之间不匹配，那么我们更新权重：w=w+yx；否则，我们让它们保持原样。

那么，为什么w=w+yx更新规则有效？因为它试图在if条件下将y(x⋅w)的值推向0的正边，从而正确地对x进行分类。如果数据集是线性可分的，通过对每个点进行一定次数的迭代，权值最终会收敛到每个点都被正确分类的状态。让我们通过在更新后重新评估if条件来查看更新规则的效果：

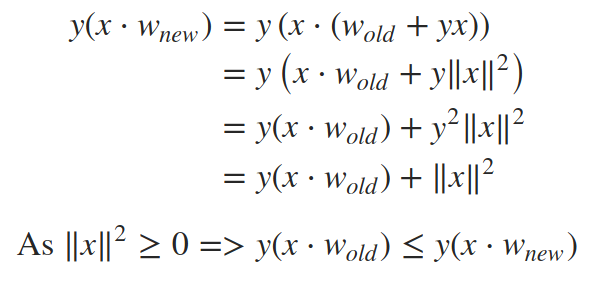
也就是说，在特定数据点的权重更新之后，if条件中的表达式应该更接近于正数，从而正确分类。

伪代码中的完整感知器算法如下：

Python实现

我们现在将在python中从头开始实现感知器算法，只使用numpy作为矩阵向量操作的外部库。我们将把它作为一个类来实现，这个类的接口类似于Scikit-Learn这样的通用机器学习包中的其他分类器。我们将为此类实现3个方法：.fit()、.predict()和.score()。

.fit()方法将用于训练感知器。它期望第一个参数是2D numpy数组X。该数组的行是数据集的样本，列是特征。第二个参数y应该是1D的numpy数组，它包含X中每行数据的标签。第三个参数n_iter是我们让算法运行的迭代次数。

def fit(self, X, y, n_iter=100):

    n_samples = X.shape[0]
    n_features = X.shape[1]

    # 偏置都加1
    self.weights = np.zeros((n_features+1,))

    X = np.concatenate([X, np.ones((n_samples, 1))], axis=1)

    for i in range(n_iter):
        for j in range(n_samples):
            if y[j]*np.dot(self.weights, X[j, :]) <= 0:
                self.weights += y[j]*X[j, :]

.predict()方法将用于预测新数据的标签。它首先检查weights对象属性是否存在，如果不存在，则表示感知器尚未训练，然后显示警告消息并返回。该方法需要一个与.fit()方法形状相同的参数X。然后我们在X和权重之间做一个矩阵乘法，然后把它们映射到-1或+1。我们使用np.vectorize()将此映射应用于矩阵乘法结果向量中的所有元素。

def predict(self, X):
    if not hasattr(self, 'weights'):
        print('The model is not trained yet!')
        return

    n_samples = X.shape[0]
    X = np.concatenate([X, np.ones((n_samples, 1))], axis=1)
    y = np.matmul(X, self.weights)
    y = np.vectorize(lambda val: 1 if val > 0 else -1)(y)

    return y

score()方法计算并返回预测的准确性。它期望输入矩阵X和标签向量y作为参数。

def score(self, X, y):
    pred_y = self.predict(X)

    return np.mean(y == pred_y)

几个例子

我现在要做的是展示几个可视化的例子，说明决策边界是如何收敛到一个解的。

为了做到这一点，我将使用ScikitLearn的datasets.make_classification()和datasets.make_circles()函数创建几个由200个样本组成的2特征分类数据集。这是用于创建下两个数据集的代码：

X, y = make_classification(
    n_features=2,
    n_classes=2,
    n_samples=200,
    n_redundant=0,
    n_clusters_per_class=1
)

还有一个数据集:

X, y = make_circles(n_samples=200, noise=0.03, factor=0.7)

对于每个示例，我将把数据分成150个用于训练，50个用于测试。左边显示训练集，右边显示测试集。当决策边界收敛到一个解决方案时，决策边界将在两边显示。但是决策边界将仅根据左边的数据(训练集)进行更新。

例1 线性可分的

我要展示的第一个数据集是线性可分的。下面是完整数据集的图像:

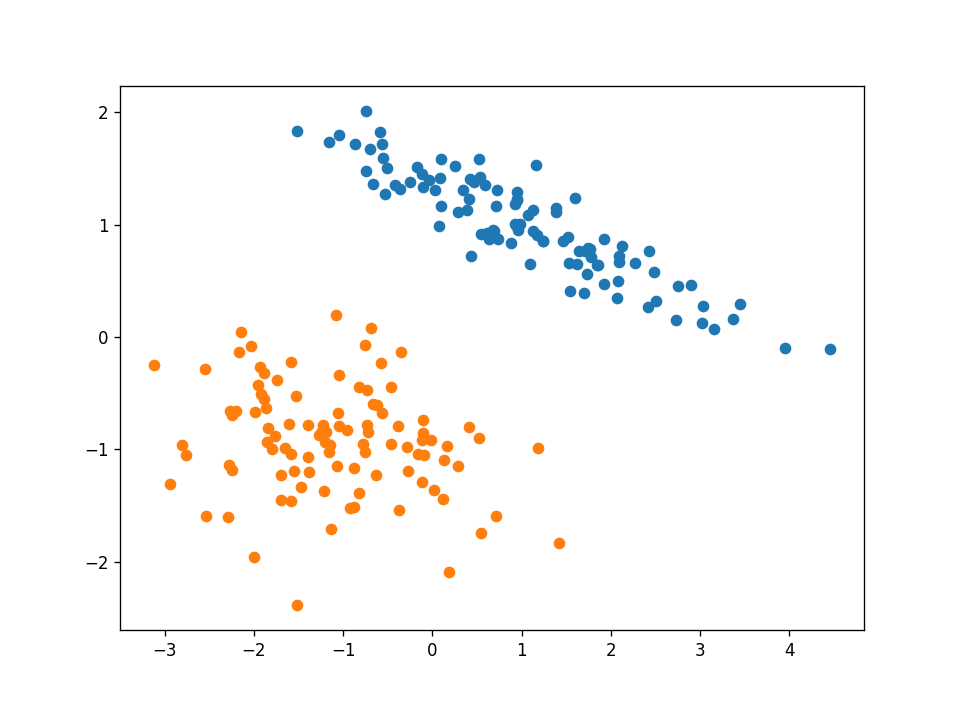
这是一个简单的数据集，我们的感知器算法在经过训练集的两次迭代后就会收敛到一个解。因此，每个数据点的动画帧都会改变。绿点是目前在算法中测试的那个。

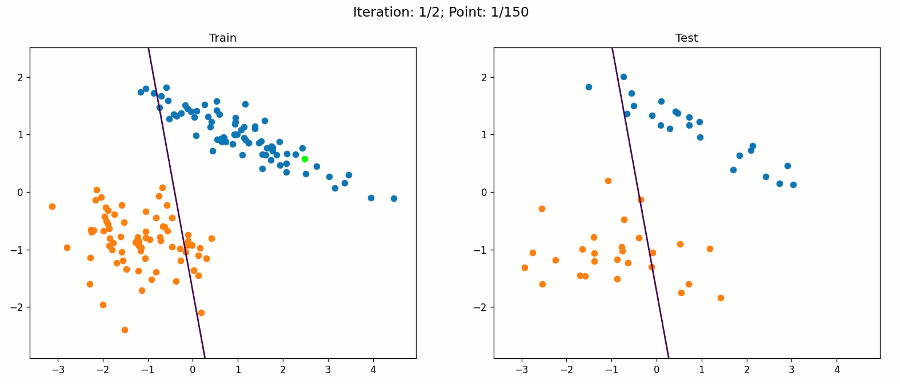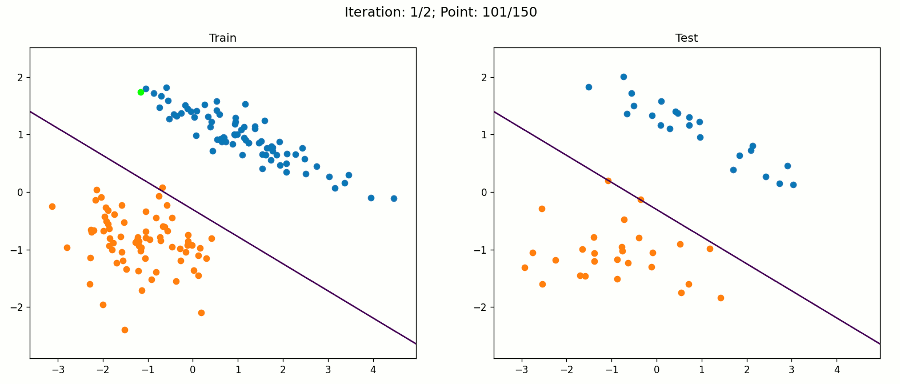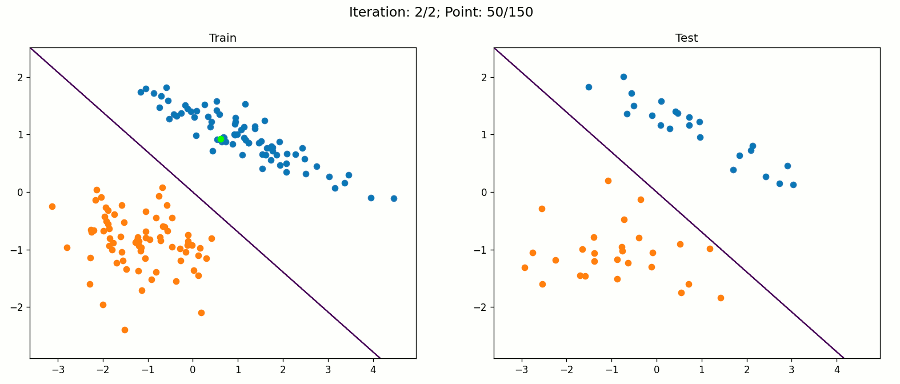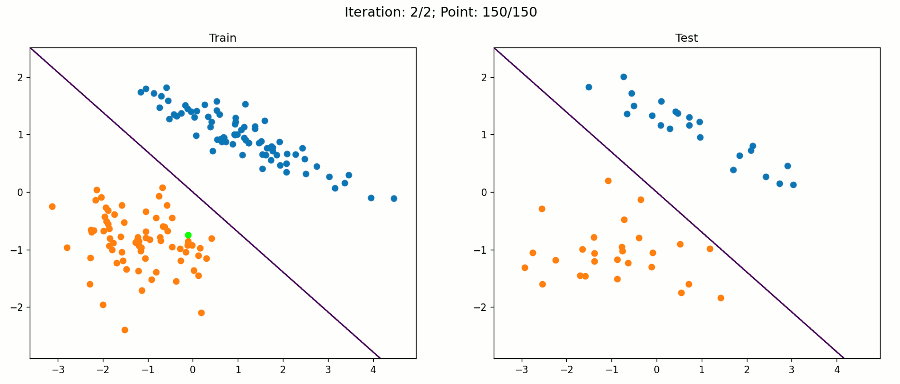
在该数据集上，算法对训练样本和测试样本进行了正确分类。

例2 噪声数据集

如果数据集不是线性可分的呢？如果正反两个例子像下图一样混淆在一起呢？

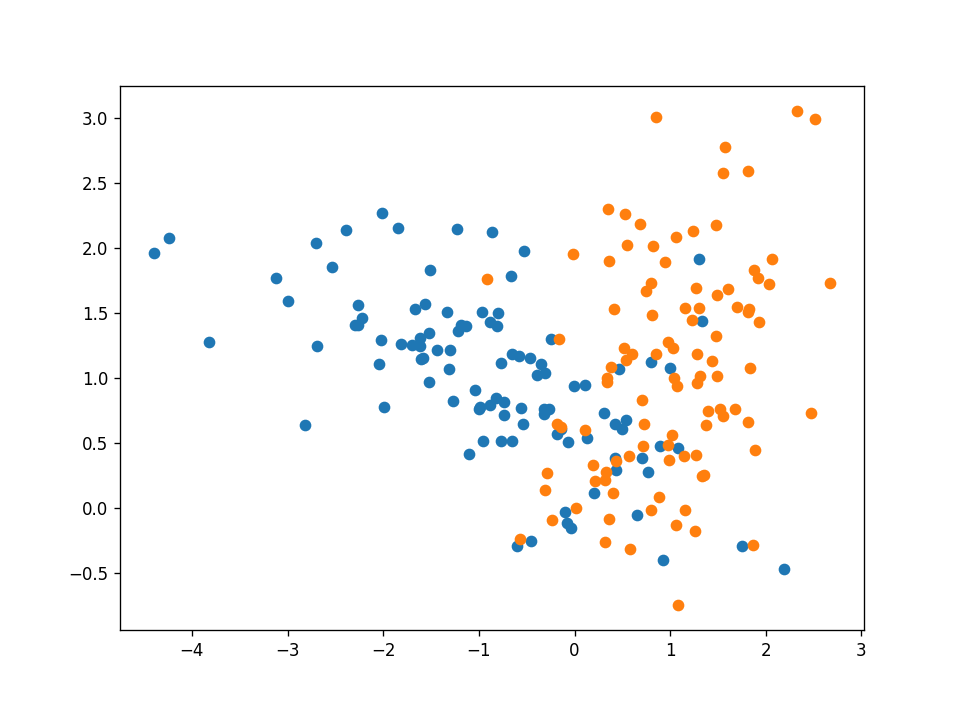
好吧，感知器算法将不能正确分类所有的例子，但它将试图找到一条线，最好的分开他们。在这个例子中，我们的感知器得到了88%的测试精度。下面的动画帧在每次迭代后都会通过所有训练示例进行更新。

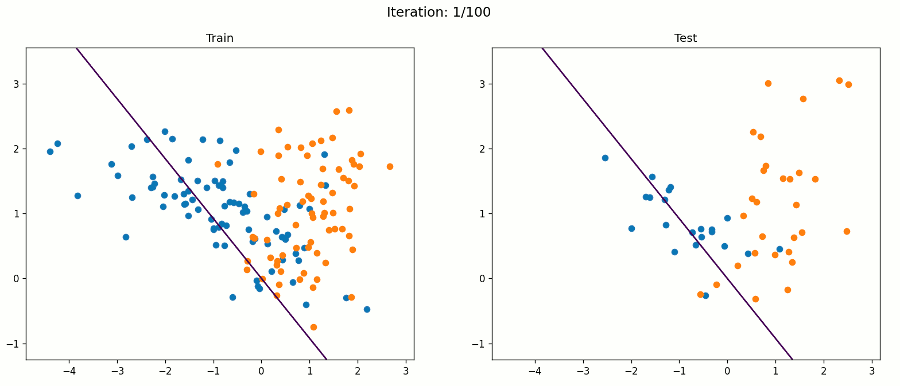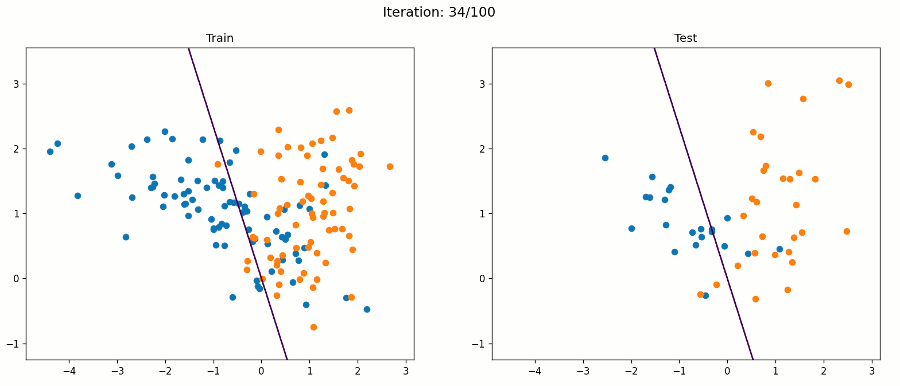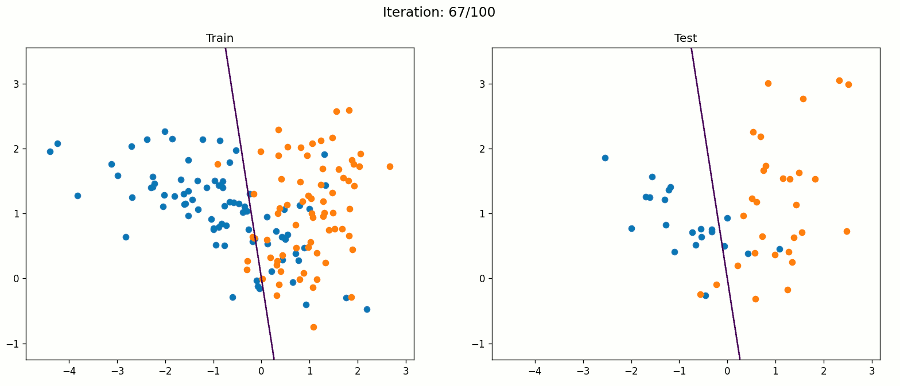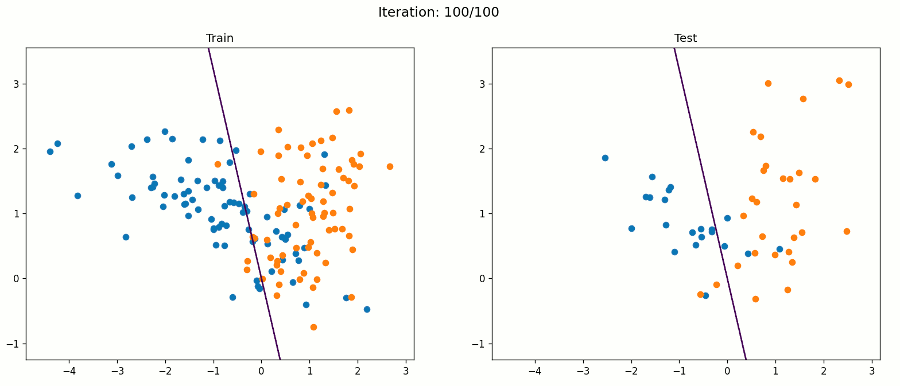
例3 非线性数据集

下面的数据集如何呢？

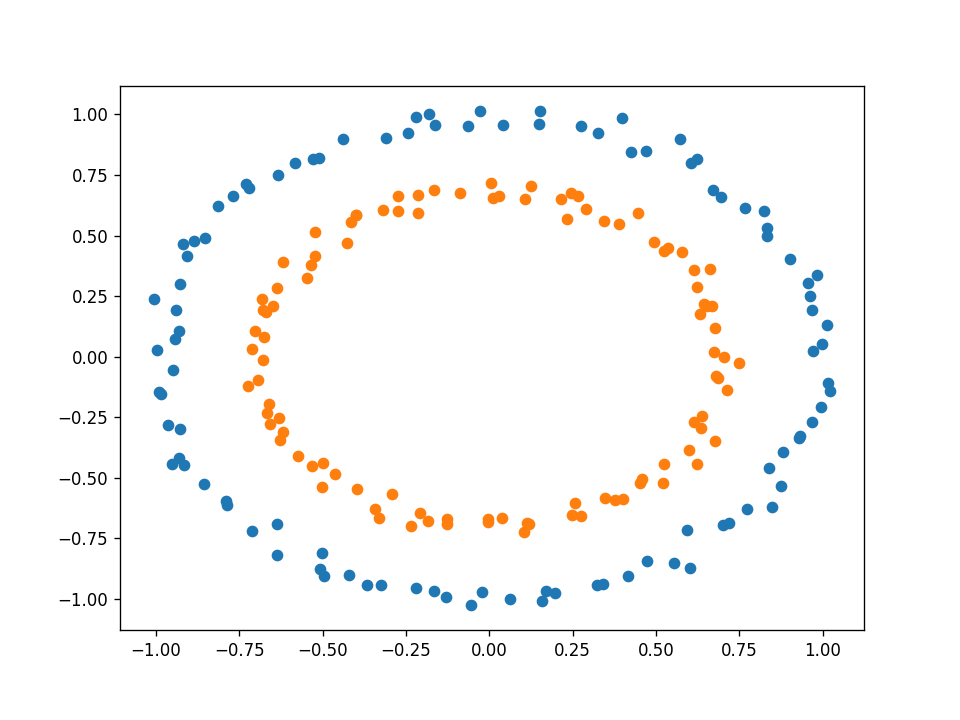
它是可分离的，但显然不是线性的。所以你可能会认为一个感知器不适合这个任务。但感知器的问题是，它的决策边界是线性的，就权重而言，不一定就输入而言。我们可以扩充输入向量x，使其包含原始输入的非线性函数。例如，除了原始输入x1和x2之外，我们还可以将项x1平方、x1乘以x2和x2平方相加。

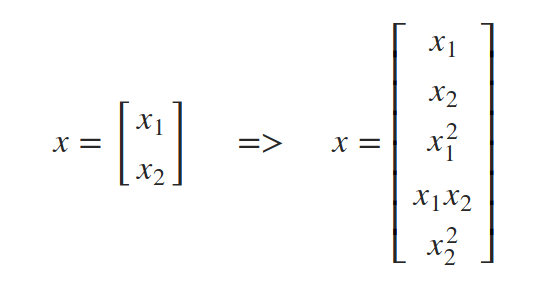
下面的 polynomial_features(X, p)(X，p)函数能够将输入矩阵X转换成一个矩阵，该矩阵包含p次多项式的所有项作为特征。它使用polynom()函数计算表示要相乘列的索引列表，以获得p阶项。

def polynom(indices_list, indices, a, b, p):
    indices = [*indices]
    if p == 0:
        indices_list.append(indices)
        return
    for i in range(a, b):
        indices.append(i)
        polynom(indices_list, indices, i, b, p-1)
        indices = indices[0:-1]

def polynomial_features(X, p):
    n, d = X.shape
    features = []
    for i in range(1, p+1):
        l = []
        polynom(l, [], 0, d, i)
        for indices in l:
            x = np.ones((n,))
            for idx in indices:
                x = x * X[:, idx]
            features.append(x)
    return np.stack(features, axis=1)

在我们的例子中，我们将在X矩阵中添加2级项作为新特征。

X = polynomial_features(X, 2)

现在，让我们看看使用这个转换后的数据集进行训练时会发生什么：

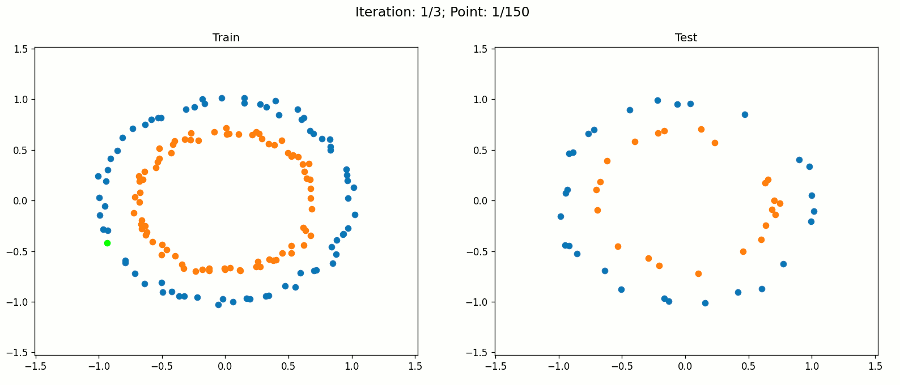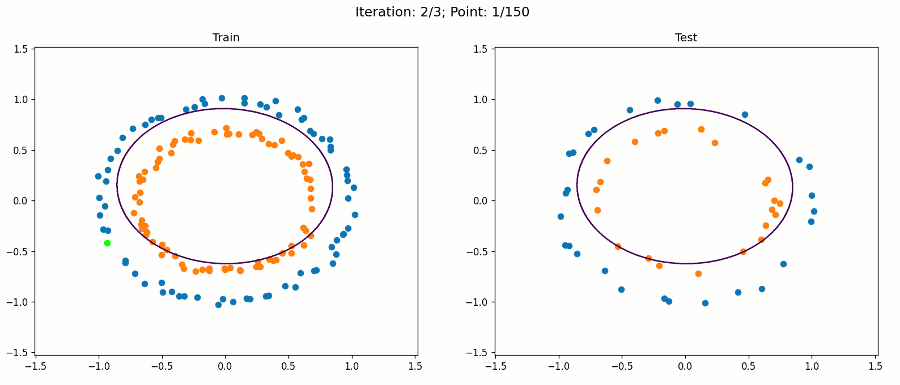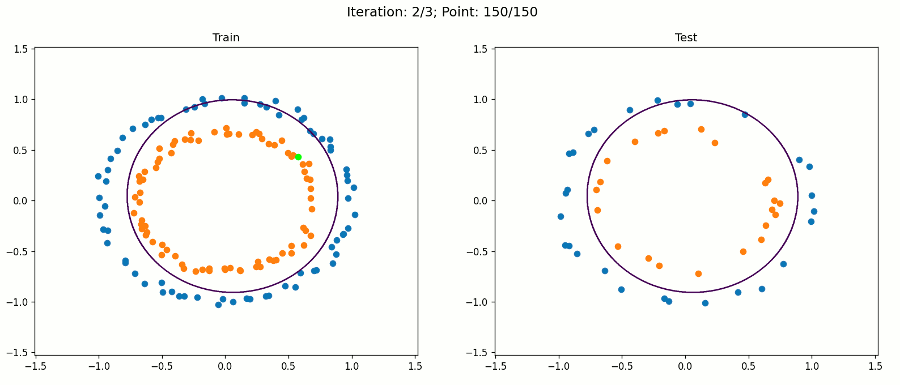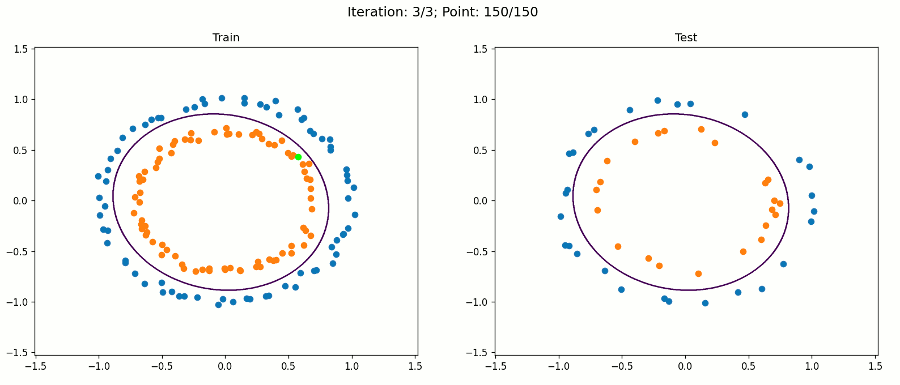
注意，对于绘图，我们只使用原始输入来保持它的二维性。决策边界在扩展特征空间中仍然是线性的，现在是5D。但是，当我们绘制投影到原始特征空间的决策边界时，它具有非线性形状。

通过这种方法，我们的感知器算法能够在不修改算法本身的情况下正确地分类训练和测试实例。我们只改变了数据集。

通过这种特征增强方法，我们可以使用线性算法在数据中建模非常复杂的模式。

但是，这种方法不是很有效。想象一下，如果我们有1000个输入特征，并且我们想用最多10次多项式项来扩充它，会发生什么。幸运的是，这个问题可以通过使用核函数来避免。但这是另一篇文章的主题，我不想把这篇文章写得太长。

原文链接：https://towardsdatascience.com/perceptron-explanation-implementation-and-a-visual-example-3c8e76b4e2d1