卷积神经网络，为什么是CNN

卷积：像素值乘以权重并求和的运算称为“卷积”。

卷积神经网络(ConvNet/CNN)是一种深度学习算法，它可以接收输入图像，为图像中的各个方面/对象分配重要性(可学习的权重和偏差)，并将它们区分开来。

通过图像分类实例，让我们了解卷积与神经网络的关系

考虑一张20×20的图像，您想要将该图像归入哪个类别(假设有4个类别，如人、汽车、飞机、花朵)。

让我们在CNN之前试着了解一下这些技巧

下面是CNN的概念

除了学习分类器的权重之外，我们是否可以学习敏感核，而不是像边缘检测器这样的手工制作的核，更有效的方法可能是学习同一层中的多个敏感核？这可以避免不合身的情况。

多层上的多个内核将会更加高效。

每一层都有多次学习卷积运算的网络称为卷积神经网络。

这与常规的神经网络有什么不同？它的好处是什么

与常规神经网络相比，cnn的主要优势是

1.稀疏连接

2.重量分担

稀疏连接

考虑包含数字2的4×4图像，我们考虑16维输入特征和10类(数字)输出。

每层可以有尽可能多的隐藏层和激活单元。

在传统的全连接前馈神经网络中，所有16维的输入都会连接到隐层，然后，隐层的每个输出都会连接到下一层。

有许多密集的连接。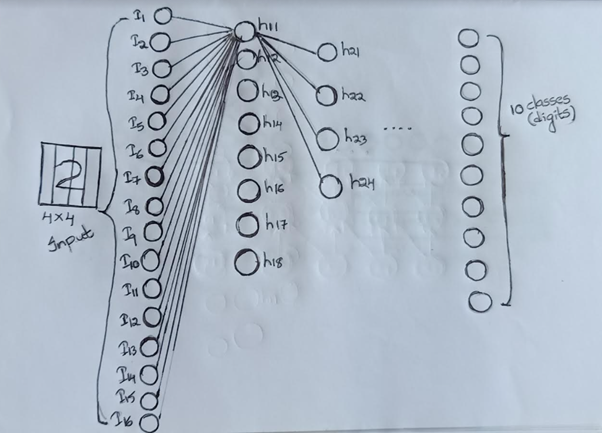

在美国有线电视新闻网(CNN)，这种联系是稀疏的。让我们清楚地理解这一点。

设H11是隐层1中的第一个神经元，在规则的前馈神经网络中，所有16个输入都对H11的计算有贡献。而在CNN中，根据核大小，只有几个输入参与。

在我们的例子中，如果我们考虑过滤的大小为2X2，步长为2，那么只有几个神经元参与H11的计算。

只有像素1、2、5、6对H11有贡献

像素3、4、7、8对h12有贡献

9，10，13，14对H13有贡献

11、12、15、16对H14做出贡献

连接比较稀疏，这里我们主要关注的是相邻像素之间的相互作用。显然，这种稀疏连接正在减少参数的数量。

但我们可能会怀疑，我们是不是失去了一些输入像素之间的交互作用，但不是真的。

让我们通过下面的示例清楚地看到这一点。

这里x1和x2像素没有相互作用，因为h2依赖于x1，x2，x3类似地，h4依赖于x3，x4，x5没有同时依赖于x1和x5的单位。

在后一层中，g3依赖于h2和h4，其中所有像素x1、x2、x3、x4、x5之间的相互作用正在发生。

尽管交互没有发生在最初的层，但随着我们深入网络，交互是显而易见的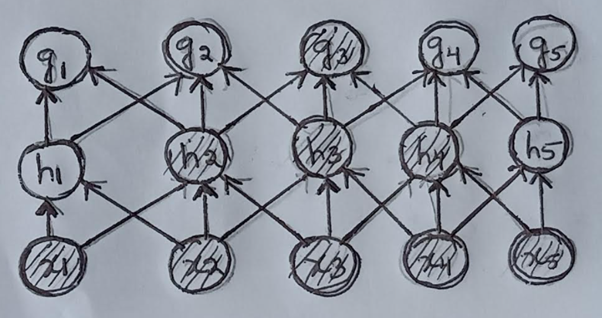

权重分担

CNN的另一个重要特点是重量共享

1.同一内核或过滤卷积全图，即我们想了解同一内核对全图的效果。

2.我们可以有许多这样的内核，但这些内核将由图像的所有位置共享

让我们来看看几个CNN的基本架构，比如LeNet、AlexNet

乐网：

这是一个5层网络，因为我们在5层有可学习的参数。

我们在这里考虑的输入图像是灰度图像32X32X1。因为它是灰度图像，所以通道数为1

对内核/过滤大小为5X5的输入图像进行卷积运算，

输入=32X32X1

内核=5×5

步距=1；填充=0

核数=6

输出=((32-5+1)X(32-5+1)X 6)

(28 X 28 X 6)

在池或子采样层中，特征地图减少了一半，而通道数保持不变。结果将是14X14X6

随后，在下一层中，我们使用5×5和16个吸核进行内核大小的卷积。卷积后的结果将是10x10x16

再次合并/二次采样图层后，要素地图将减少一半。因此，这里的结果可能是5x5x16

对上述过滤大小为5×5的结果进行进一步的卷积运算，使用并进一步展平这样的核。然后是2个完全连接的层。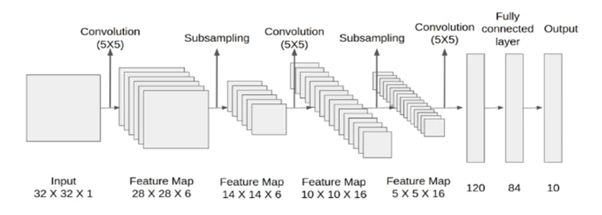

下面的表格格式对架构细节进行了进一步的详细说明。

学习的参数数量按以下方式计算。

让我们为LeNet架构编写python代码

import tensorflow as tf

正在加载数据

(train_x, train_y), (test_x, test_y) = keras.datasets.mnist.load_data()

创建LeNet模型体系结构

lenet_5_model = keras.models.Sequential([

编译模型

lenet_5_model.compile(optimizer='adam',loss=keras.losses.sparse_categorical_crossentropy,metrics=['accuracy'])

拟合模型

lenet_5_model.fit(train_x, train_y, epochs=5, validation_data=(val_x, val_y))

lenet_5_model.evaluate(test_x, test_y)

lenet_5_model.summary()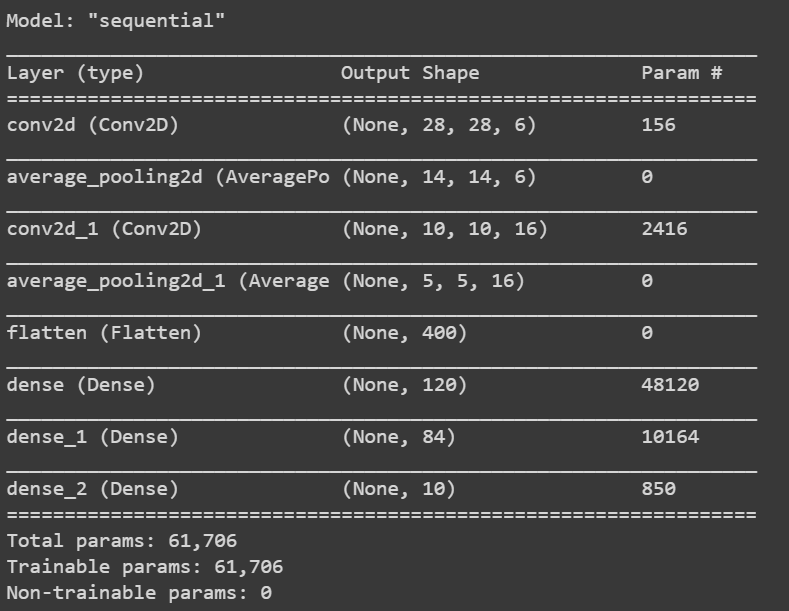

AlexNet：

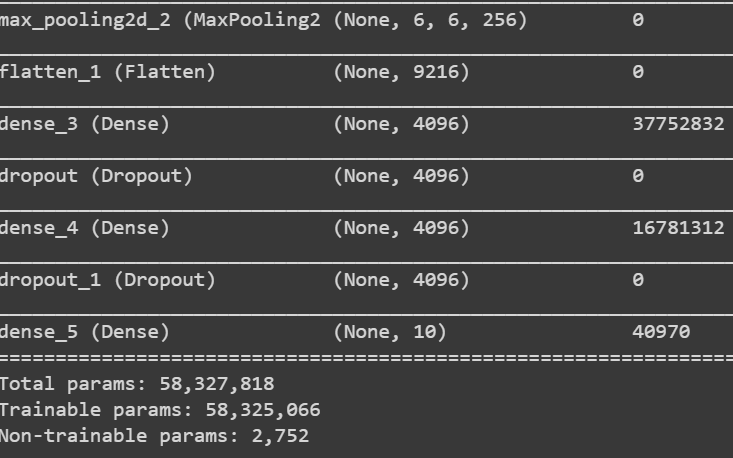
AlexNet是一个8层网络，因为我们在8层有可学习的参数。它由5个卷积层，3个全连通层组成。

可学习参数总数为6200万

下面是AlexNet的架构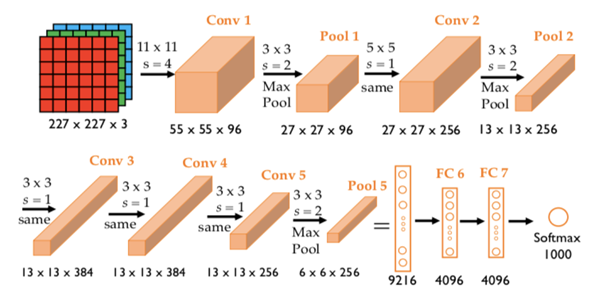

如果将227x227x3的输入图层图像与96个核进行卷积，每个核的大小为11×11，则结果为((227-11)/4+1)x(227-11)/4+1)x96)=55X55X96

上面的结果被传递到池层，这会减少传递的输入，这里我们考虑使用3×3过滤进行池化。最大池化后的结果为((55-3)/2+1)x(55-3)/2+1)x 96)=27 x 27 x 96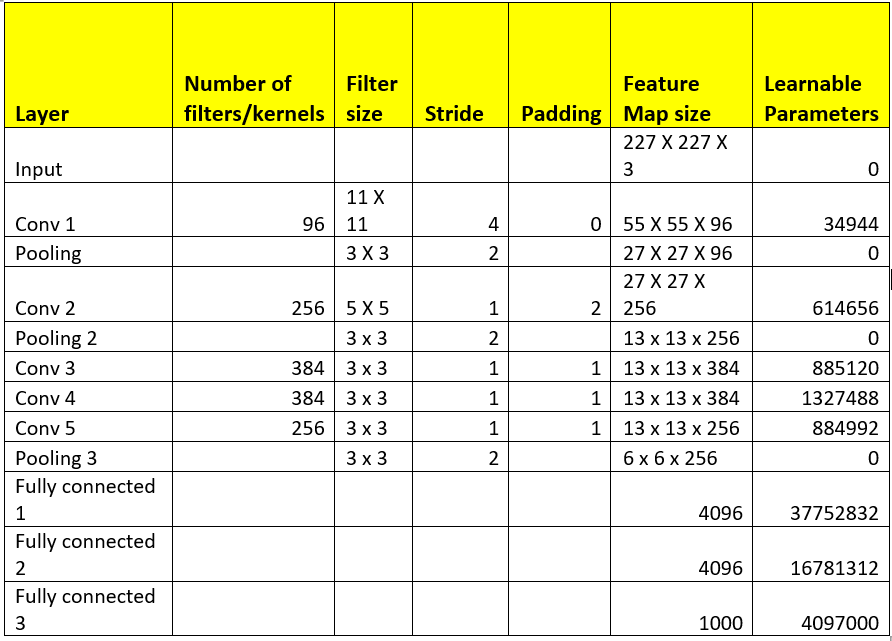

就像LeNet代码一样，我们可以构建AlexNet的体系结构，并在调整大小后将其适合于输入图像

下面是构建AlexNet架构的分步过程。

Alexnet = keras.models.Sequential([

型号摘要

Alexnet.summary()