作者|Krunal Kshirsagar
编译|Flin
来源|Medium
什么是SLAM?
即时定位与地图构建(simultaneous localization and mapping,简写成SLAM),用于环境模型(map)的并行构建,以及在其中移动的机器人的状态估算。换句话说,SLAM为你提供了一种实时跟踪机器人在世界上的位置、并识别地标(例如建筑物,树木,岩石和其他世界特征)的位置的方法。除了本地化之外,我们还希望建立机器人环境的模型,这样我们就有了一个物体的概念,以及围绕机器人的地标,以便我们可以使用此地图数据来确保机器人在世界各地移动时走在正确的道路上。因此,构建地图的关键是机器人本身可能会由于其运动不确定性而失去对其位置的跟踪,因为不存在现有的地图,并且我们正在用机器人并行构建地图。而这就是SLAM发挥作用的地方。
SLAM的工作:
同时定位和地图绘制(SLAM)的基础是从机器人的传感器和随时间推移的运动中收集信息,然后使用有关测量和运动的信息来重建世界地图。在这种情况下,我们将机器人定位在2D网格世界中,因此,基于图的SLAM方法通过提取原始传感器测量值来构造简化的估计问题。这些原始测量值将替换为图中的边缘,然后可以将其视为虚拟测量值。
假设我们有一个机器人和初始位置 x0 = 0 和 y0 = 0 。对于此示例,为了保持简单,我们并不关心方向。让我们假设机器人在X方向上向右移动了10。所以,在理想世界中,你会了解到 x1,运动后的位置与x0 + 10相同,即x1 = x0 + 10,同理,y1与y0相同。
如图,机器人在x方向上的位移为10:

但是根据卡尔曼滤波器(https://medium.com/@krunalkshirsagar/the-curious-case-of-kalman-filters-f29c3d17b121) 和其他各种机器人技术,我们已经知道位置实际上是不确定的。因此,与其假设我们的XY坐标系中的机器人精确地向右移动了10个位置,不如理解成它在x1 = x0 + 10运动更新后的实际位置是以(10,0)为中心的高斯分布,但是机器人也可能在其他地方。
如图:运动更新后,高斯以机器人的位置为中心
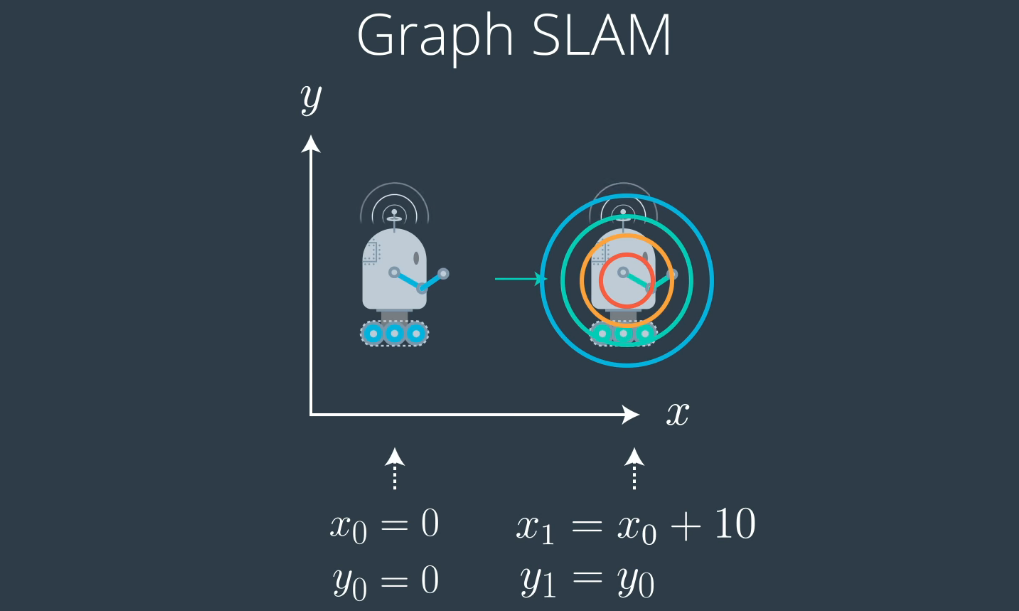
这是x变量的高斯的数学公式:
当这两个条件相同时,与其将x1设置为x0+10,不如用高斯函数来表示,此时高斯函数达到峰值。。因此,如果你减去x1-x0-10,把它变成一个正方形,然后将其转换为高斯,我们将得到与x1和x0相关的概率分布。我们可以对y做同样的转换。根据我们的运动y不变,因此y1和y0尽可能靠近。
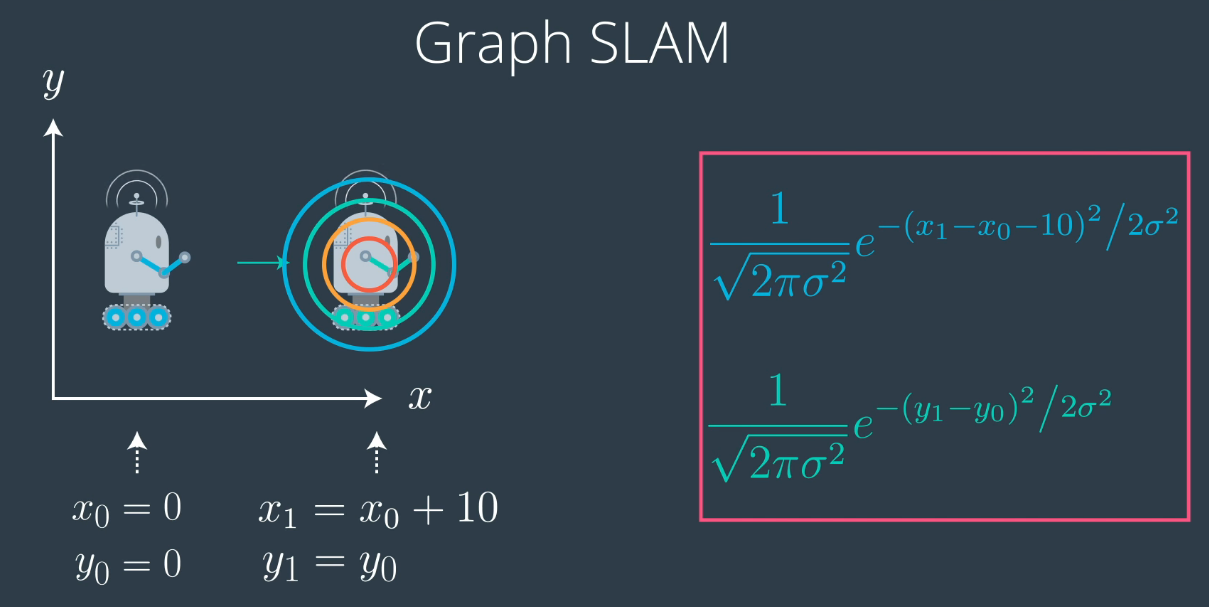
这两个高斯的乘积现在是我们的约束条件。目标是在位置x0为(0,0)的情况下最大化位置x1的可能性。因此,Graph SLAM所做的是,它使用一系列此类约束条件来定义概率。 假设我们有一个在某个空间中移动的机器人,GRAPH SLAM会收集其初始位置(0,0),最初也称为“初始约束”,然后收集许多相对约束,这些相对约束会将每个机器人姿态与之前的机器人姿态相关联作为相对运动约束。例如,让我们使用机器人可以在各个位置看到的地标,这是每次机器人看到地标时的相对测量约束。因此,Graph SLAM收集这些约束,以便找到最可能的机器人路径配置以及地标位置,即映射过程。
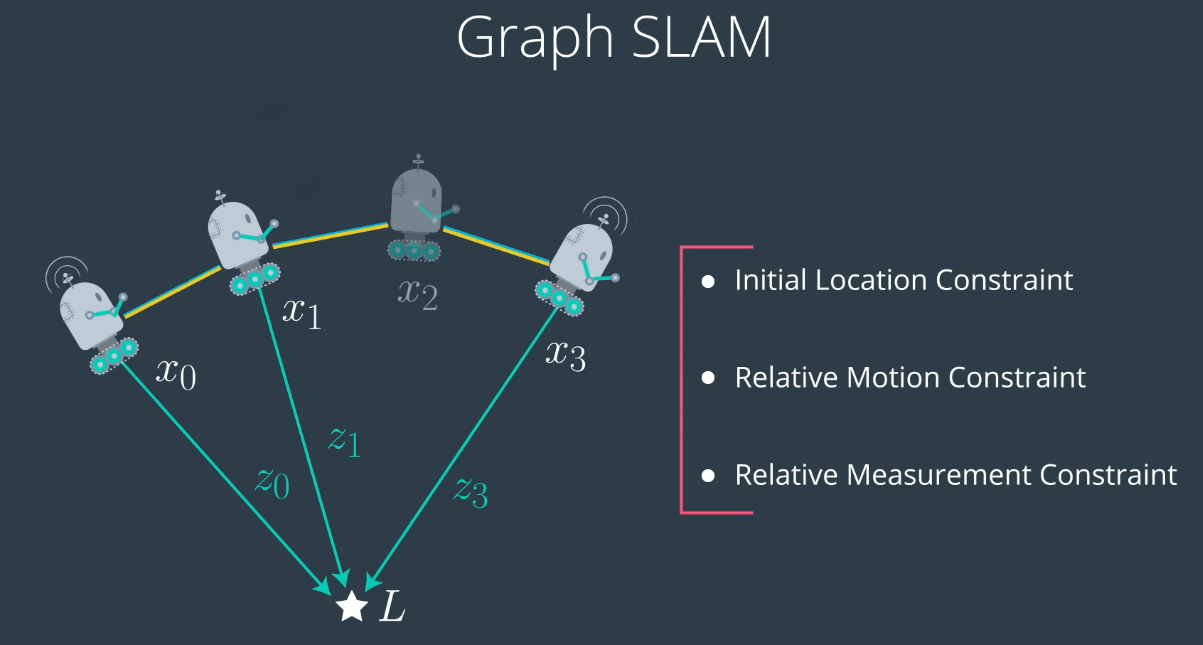
实作
生成环境:
我们将生成一个带有地标的2D世界网格,然后通过将机器人放置在该世界中,并在一定数量的时间步长上移动和感应来生成数据。实例化的机器人在世界中移动和感知时,将收集数据。我们的SLAM函数将把这些数据作为输入。因此,让我们首先创建此数据,并探索它如何代表我们的机器人进行运动和传感器测量。
SLAM输入:
除了数据之外,我们的slam函数还具有:
- N:机器人将要移动和感应的时间步数。
- num_landmarks:世界上的地标数量。
- world_size:你的世界的大小(w / h)。
- motion_noise:与运动相关的噪声;运动的更新置信度应为
1.0/motion_noise. - measurement_noise:与测量/传感相关的噪声;测量的更新权重应为
1.0/measurement_noise.
import numpy as np
from helpers import make_data
#slam的实现应该使用以下输入
#请随意更改这些输入值并查看其响应方式!
# 世界参数
num_landmarks = 5 # number of landmarks
N = 20 # time steps
world_size = 100.0 # size of world (square)
# 机器人参数
measurement_range = 50.0 # range at which we can sense landmarks
motion_noise = 2.0 # noise in robot motion
measurement_noise = 2.0 # noise in the measurements
distance = 20.0 # distance by which robot (intends to) move each iteratation
# make_data实例化一个机器人,并为给定的世界大小和给定数量的地标生成随机地标
data = make_data(N, num_landmarks, world_size, measurement_range, motion_noise, measurement_noise, distance)
让我们编写两个主要功能,这些功能可以使机器人四处移动,帮助定位地标并在2D地图上测量它们之间的距离:
- Move:尝试按dx,dy移动机器人。
-
Sense:返回可见范围内地标的x和y距离。
class robot: #move function def move(self, dx, dy): x = self.x + dx + self.rand() * self.motion_noise y = self.y + dy + self.rand() * self.motion_noise if x < 0.0 or x > self.world_size or y < 0.0 or y > self.world_size: return False else: self.x = x self.y = y return True #sense function def sense(self): measurements = [] for landmark_index, landmark in enumerate(self.landmarks): landmark_distance_x = landmark[0] landmark_distance_y = landmark[1] random_noise = self.rand() cal_dx = self.x - landmark_distance_x + random_noise * self.measurement_noise cal_dy = self.y - landmark_distance_y + random_noise * self.measurement_noise is_not_in_measurement_range = self.measurement_range == -1 if(is_not_in_measurement_range) or ((abs(cal_dx) <= self.measurement_range) and (abs(cal_dy) <= self.measurement_range)): measurements.append([landmark_index, cal_dx, cal_dy]) return measurements
Omega 和 Xi:
为了实现Graph SLAM,引入了一个矩阵和一个向量(分别为ω和xi)。矩阵是正方形的,标有所有机器人姿势(xi)和所有地标。例如,每次进行观察时,当你在两个姿势之间移动某个距离dx,并可以关联这两个位置时,可以将其表示为这些矩阵中的数值关系。
让我们编写函数,以便它为机器人的起始位置返回omega和xi约束。我们尚不知道的所有值都应使用0进行初始化。我们可以假设我们的机器人以100%的置信度在世界的正中间开始。
def initialize_constraints(N, num_landmarks, world_size):
''' This function takes in a number of time steps N, number of landmarks, and a world_size,
and returns initialized constraint matrices, omega and xi.'''
middle_of_the_world = world_size / 2
## 建议:在变量中定义和存储约束矩阵的大小(行/列)
rows, cols = 2*(N + num_landmarks), 2*(N + num_landmarks)
## TODO: 用两个初始“strength”值定义约束矩阵Omega
omega = np.zeros(shape = (rows, cols))
## 我们机器人最初的x,y位置
#omega = [0]
omega[0][0], omega[1][1] = 1,1
## TODO: Define the constraint *vector*, xi
## 假设机器人以100%的置信度在世界的正中间开始。
#xi = [0]
xi = np.zeros(shape = (rows, 1))
xi[0][0] = middle_of_the_world
xi[1][0] = middle_of_the_world
return omega, xi通过运动和测量值进行更新:
## slam接受6个参数并返回mu,
## mu是机器人穿过的整个路径(所有x,y姿势)和所有地标位置
def slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise):
## TODO: 使用你的初始化创建约束矩阵
omega, xi = initialize_constraints(N, num_landmarks, world_size)
## TODO:遍历数据中的每个时间步骤
for time_step in range(len(data)):
## 每次迭代时获取所有的运动和测量数据
measurement = data[time_step][0]
motion = data[time_step][1]
x
dx = motion[0] # 本次沿x移动的距离
dy = motion[1] # 本次沿y移动的距离
#假设机器人在这个时间从(x0,y0)移动到(x1,y1)
#omega的偶数列对应于x值
x0 = (time_step * 2) #x0 = 0,2,4,...
x1 = x0 + 2 #x1 = 2,4,6,...
# omega 的奇数列对应于y值
y0 = x0 + 1 #y0 = 1,3,5,...
y1 = y0 + 2 #y1 = 3,5,7,...
actual_m_noise = 1.0/measurement_noise
actual_n_noise = 1.0/motion_noise
## TODO: 更新约束矩阵/向量(Omega/xi)以解释所有*measurements*
## 这应该是一系列考虑测量噪声的附加值
for landmark in measurement:
lM = landmark[0] # 地标 id
dx_lM = landmark[1] # 沿x与当前位置分离
dy_lM = landmark[2] # 沿y与当前位置分离
L_x0 = (N*2) + (lM*2) # 偶数列有x个地标值
L_y0 = L_x0 + 1 # 奇数列有y个地标值
# 更新对应于x0和Lx0之间测量值的omega值
omega[x0][x0] += actual_m_noise
omega[L_x0][L_x0] += actual_m_noise
omega[x0][L_x0] += -actual_m_noise
omega[L_x0][x0] += -actual_m_noise
# 更新对应于y0和Ly0之间测量值的omega值
omega[y0][y0] += actual_m_noise
omega[L_y0][L_y0] += actual_m_noise
omega[y0][L_y0] += -actual_m_noise
omega[L_y0][y0] += -actual_m_noise
# 更新X0和LX0之间的测量值对应的xi值
xi[x0] -= dx_lM/measurement_noise
xi[L_x0] += dx_lM/measurement_noise
# 更新y0和Ly0之间的测量值对应的xi值
xi[y0] -= dy_lM/measurement_noise
xi[L_y0] += dy_lM/measurement_noise
## TODO: 更新约束矩阵/向量(omega/XI),以解释从(x0,y0)到(x1,y1)和运动噪声的所有*运动*。
omega[x0][x0] += actual_n_noise
omega[x1][x1] += actual_n_noise
omega[x0][x1] += -actual_n_noise
omega[x1][x0] += -actual_n_noise
omega[y0][y0] += actual_n_noise
omega[y1][y1] += actual_n_noise
omega[y0][y1] += -actual_n_noise
omega[y1][y0] += -actual_n_noise
xi[x0] -= dx/motion_noise
xi[y0] -= dy/motion_noise
xi[x1] += dx/motion_noise
xi[y1] += dy/motion_noise
## TODO: 在遍历所有数据之后
## 计算姿势和地标位置的最佳估计值
##使用公式,omega_inverse * Xi
inverse_of_omega = np.linalg.inv(np.matrix(omega))
mu = inverse_of_omega * xi
return mu机器人的姿势和地标:
让我们打印函数产生的估计姿势和界标位置。我们定义了一个提取姿势和地标位置,并将它们作为自己的单独列表返回。
def get_poses_landmarks(mu, N):
# 创建一个姿势列表
poses = []
for i in range(N):
poses.append((mu[2*i].item(), mu[2*i+1].item()))
# 创建一个地标列表
landmarks = []
for i in range(num_landmarks):
landmarks.append((mu[2*(N+i)].item(), mu[2*(N+i)+1].item()))
# 返回完成的列表
return poses, landmarks
def print_all(poses, landmarks):
print('\n')
print('Estimated Poses:')
for i in range(len(poses)):
print('['+', '.join('%.3f'%p for p in poses[i])+']')
print('\n')
print('Estimated Landmarks:')
for i in range(len(landmarks)):
print('['+', '.join('%.3f'%l for l in landmarks[i])+']')
# 调用你的slam实现,并传入必要的参数
mu = slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
# 打印出地标和姿势结果
if(mu is not None):
# 获取姿势和地标列表
# 并打印出来
poses, landmarks = get_poses_landmarks(mu, N)
print_all(poses, landmarks)如图:估计的机器人姿势和地标

可视化构建的世界:
# 导入函数
from helpers import display_world
# 显示最终世界!
# 定义图形大小
plt.rcParams["figure.figsize"] = (20,20)
# 检查姿势是否已创建
if 'poses' in locals():
# 打印出最后一个姿势
print('Last pose: ', poses[-1])
# 显示机器人的最后位置和地标位置
display_world(int(world_size), poses[-1], landmarks)如图:输出量
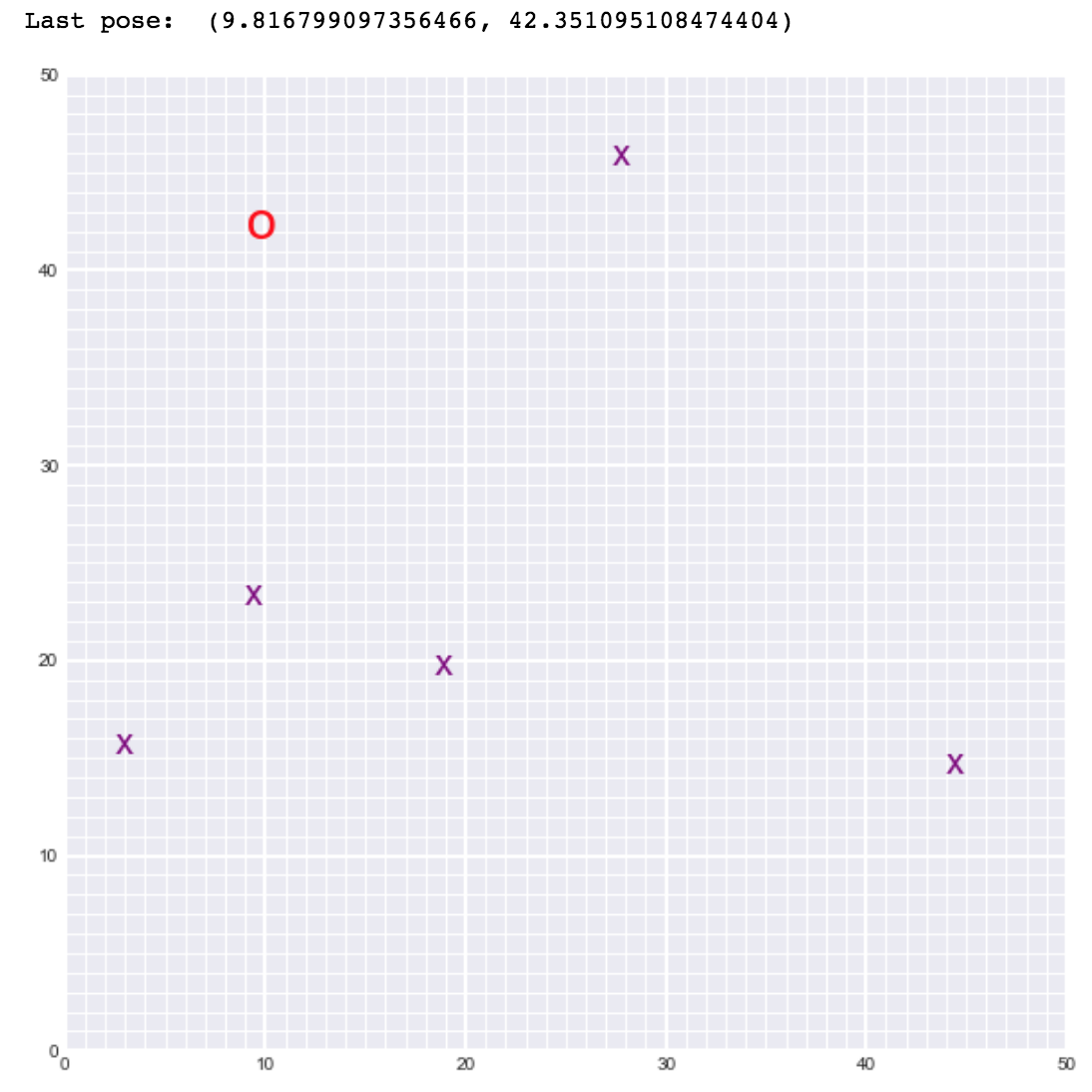
在Github(https://github.com/Noob-can-Compile/Landmark_Detection_Robot_Tracking_SLAM-) 上检查代码。
欢迎关注磐创AI博客站:
http://panchuang.net/
sklearn机器学习中文官方文档:
http://sklearn123.com/
欢迎关注磐创博客资源汇总站:
http://docs.panchuang.net/
原创文章,作者:磐石,如若转载,请注明出处:https://panchuang.net/2020/09/01/%e5%9b%beslam%ef%bc%9anoob%e7%9a%84%e5%90%8c%e6%97%b6%e6%9c%ac%e5%9c%b0%e5%8c%96%e5%92%8c%e6%98%a0%e5%b0%84%e6%8c%87%e5%8d%97/

