粒子过滤是一种定位算法,基于对随机点进行采样并计算您的点代表被跟踪对象的真实位置的概率。在这个实现中,我使用python创建了一个模拟环境,它包含以下功能:
这篇文章更多的是关于我的优化,而不是一个粒子过滤的介绍。虽然我将简要概述该系统的工作原理,但要获得更全面的概述,我会阅读其他资源。other resources
颗粒过滤
粒子过滤是一种用于各种计算领域的算法,如认知计算和信号处理。它最初是由Del Moral于1996年发展起来的[1],它的名字指的是自1960年™以来在流体力学中使用的概率方程,1998年也被刘和陈进一步归类为序贯蒙特卡罗方法[2]。
该特定应用和示例表示粒子过滤器可以在计算机视觉应用中使用的常见方式。在™最简单的形式中,粒子过滤包括随机抽样一组可能的解,根据某种形式的观测计算每个解正确的概率,然后根据旧的集对新的一组进行重新采样,然后重复进行以得出更准确的估计。
如果您更喜欢快速直观的解释,这里有几帧我的算法在运行中。
在初始状态下,我们在地图上生成一个随机位置。该位置由一个深蓝色圆圈和一个白色轮廓标记。在第一步中,我们在地图上生成N个随机均匀分布的点,以估计我们认为无人机在哪里。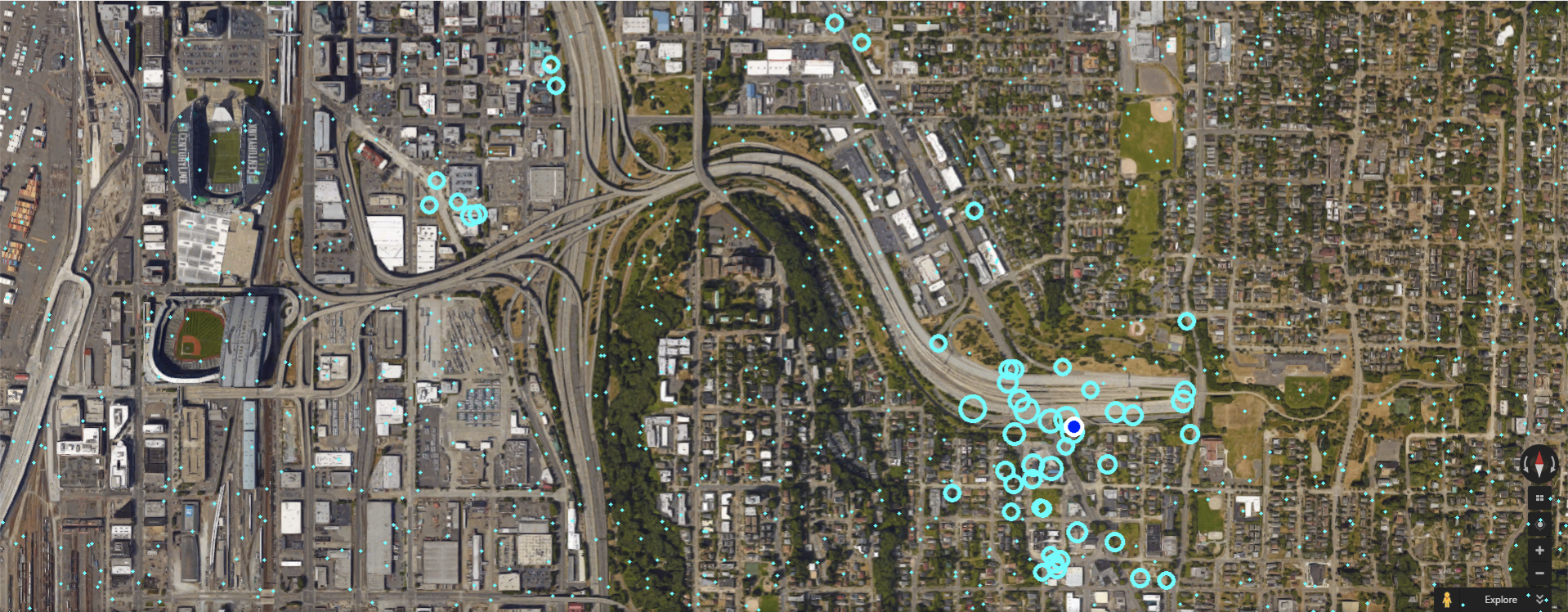
这些粒子用浅蓝色圆圈标记。在我的应用程序中,圆的半径表示随机选择的点是无人机位置的概率。所以在这里我们可以看到无人机可能在几个地方。一个时间步长绝对不足以定位无人机。
现在,从这里开始的每一个时间步,我们都会对粒子重新采样。分布较高的粒子更有可能被选中。然后我们重新计算每个重采样点的概率。我们还在重采样中添加了一点噪波,即相对于原始采样点的x,y偏移。
从这里,我们可以看到,第二个时间步长极大地改进了我们对位置的估计。我们在第一步的每个圆圈周围重新采样了几个粒子,这些粒子被认为是极有可能的。我们还知道无人机的速度,所以在重新采样后,我们可以以与无人机相同的速度移动所有粒子。在那之后,我们重新计算给定粒子的新位置的概率,我们可以看到算法能够进一步缩小范围。
我们将在本文后面介绍如何计算概率以及如何改进基本功能。
如何运行脚本
从我的存储库下载存储库,导航到名为-EuropythonSimulationEnvironment?œ�的目录,然后在命令行上运行python3SimulationEngine.py(您必须已经安装了Python3)。要在本地运行它,您需要一些库。我没有收集所有必要的库,但最重要的是Numpy和OpenCV。有很多在线指南可以安装它们,但是我对这两个都使用了-uroœpip install-euro�命令。my repository
实施
无人机运动
无人机移动基于随机生成的向量,并通过计算限制其将无人机推出地图网格。首先,我根据网格、当前位置和速度大小计算运动的极限为[Xmin,xmax],[Ymin,Ymax]。然后我运行以下计算:
每秒钟都会产生一个新的速度,它决定了无人机和粒子的运动。然而,无人机也有噪音计算。这是利用从每个x和y位置的正态分布中选择的随机值来实现的。与速度矢量类似,在应用噪波之前,我们检查运动边界,并且只生成不会使我们越过地图边缘的噪波(Won-uro™t put of the map)。对于大多数测试,我使用0.2个位置单位的方差平方。我这样做是因为我发现较小的方差有助于我更快地进行本地化,而0.2似乎是发动机和温和风产生的噪声值的真实值。
位置生成
初始无人机位置生成使用与粒子位置生成相同的代码。这是非常基本的,只是从均匀分布中获取一个值,在MAP-uro™的边界内的某个地方。
粒子量的计算和移动
我的特定过滤中最复杂的部分是粒子的权重计算。因为这里发生的事情很多,所以我会一步一步地进行权重计算。
粒子位置再生
在我们计算了粒子位置之后,我们可以对粒子重新采样,以缩小哪些粒子最有可能代表我们的位置。在我的系统中,粒子重新生成发生在图像显示之后,所以它是主函数的每个循环中发生的第一件事。在这个项目中,我使用了低方差采样器算法,取自Thrun、Burgard和Foxâuro™的教科书[3]。
当我计算权重时,我利用了重采样器的一些功能,但是唯一没有在教科书中描述的是我的重采样噪波生成(™)。当我重新生成噪波粒子时,我在重新生成过程中添加了一些变化,以解决无人机速度的误差,并增加无人机™位置的初始计算区域。(=
噪声以速度矢量的形式生成,其中x和y速度都是从正态分布中选择的,其方差与前一步中的粒子权重成反比。我还有一个缩放参数来影响所有粒子的噪波重新生成。方程式看起来有点像这样:
Xvel = N(0, ((1 - ωadj) * F) 2)
Yvel = N(0, ((1 - ωadj) * F) 2)在这里的代码中可以找到Found here in the code
使用权重的倒数的目的是使概率较高的粒子ğ�‘ƒ(ğ�’§ğ�‘|ğ�’袁ğ�‘’)在再生时具有较小的方差。如果粒子的权重接近1,则噪波可以忽略不计。值得一提的是,我没有使用常规的权重,而是使用了™™-,这是我的自定义调整后的权重,也就是众所周知的视觉权重(VisualWeight)。F是参数化比例因子。我最优化的版本使用0.8的比例因子。理想情况下,较低的因子意味着最终结果将更精确,但是,它也会降低我们在前几步定位到粒子的机会,并且如果过滤在任何给定步骤中给粒子以高速噪波,则过滤很容易丢失粒子的位置。
观察
测量
那么,我们如何从数学上衡量我们的粒子有多精确呢?我选择了两条路线,绝对平均偏差(我主要将其称为偏差)和方差。在现实世界中,如果没有实际位置,绝对平均偏差将无法测量,方差将是一个更好的选择,但我们可以使用它,因为它是一个模拟的™。我使用的偏差公式是:absolute average deviation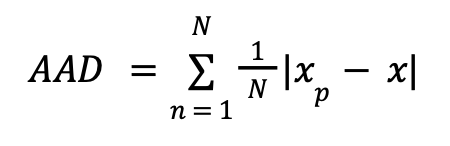
在此等式中,xp是粒子位置,xx是实际靶标位置。
对于方差,我使用Numpyâuro™的内置方差函数。我取位置和重量的方差。对于权重,我取一个填充了权重值的数组的方差;对于位置,我取一个填充了X值的数组的方差,以及一个填充了Y值的数组的方差,然后对这些方差执行毕达哥拉斯定理,以获得总的位置方差。
此处的指标函数Metrics function here
初始测试
我想测试一下我最初的过滤,然后在上面迭代,试图减少差异和偏差。我从500个粒子,50像素光圈,移动幅度为1开始,并使用直方图交集作为我的比较函数
这个测试非常能说明过滤在初期测试中的表现:
第一个状态已经显示了此设置的故障。整个图像上没有太多粒子。虽然我们很幸运,在无人机的正上方产生了一个粒子,但无人机可能存在的许多区域附近没有粒子。在5个步骤之后,粒子将移动到以下位置:
到目前为止,无人机只在陆地上空飞行,它在地图上显示,我们几乎已经清除了水面上的所有粒子。然而,我们还没有完全定位粒子™。它在南部附近的森林和建筑区上空飞行,我不认为它会有足够的本地化程度来使用。在运行了10多个步骤之后,我可以看到这是一个相当准确的假设。
在这里我们可以看到,无人机周围已经聚集了很多颗粒物,但是在港口东侧的主要城镇还有很多其他的颗粒物,西南方向的森林里还有一些颗粒物。实际上,粒子™根本没有本地化,即使经过了15个单位的时间,系统在这次迭代中也是相当无用的。下面我画出每个步骤中粒子的方差和偏差: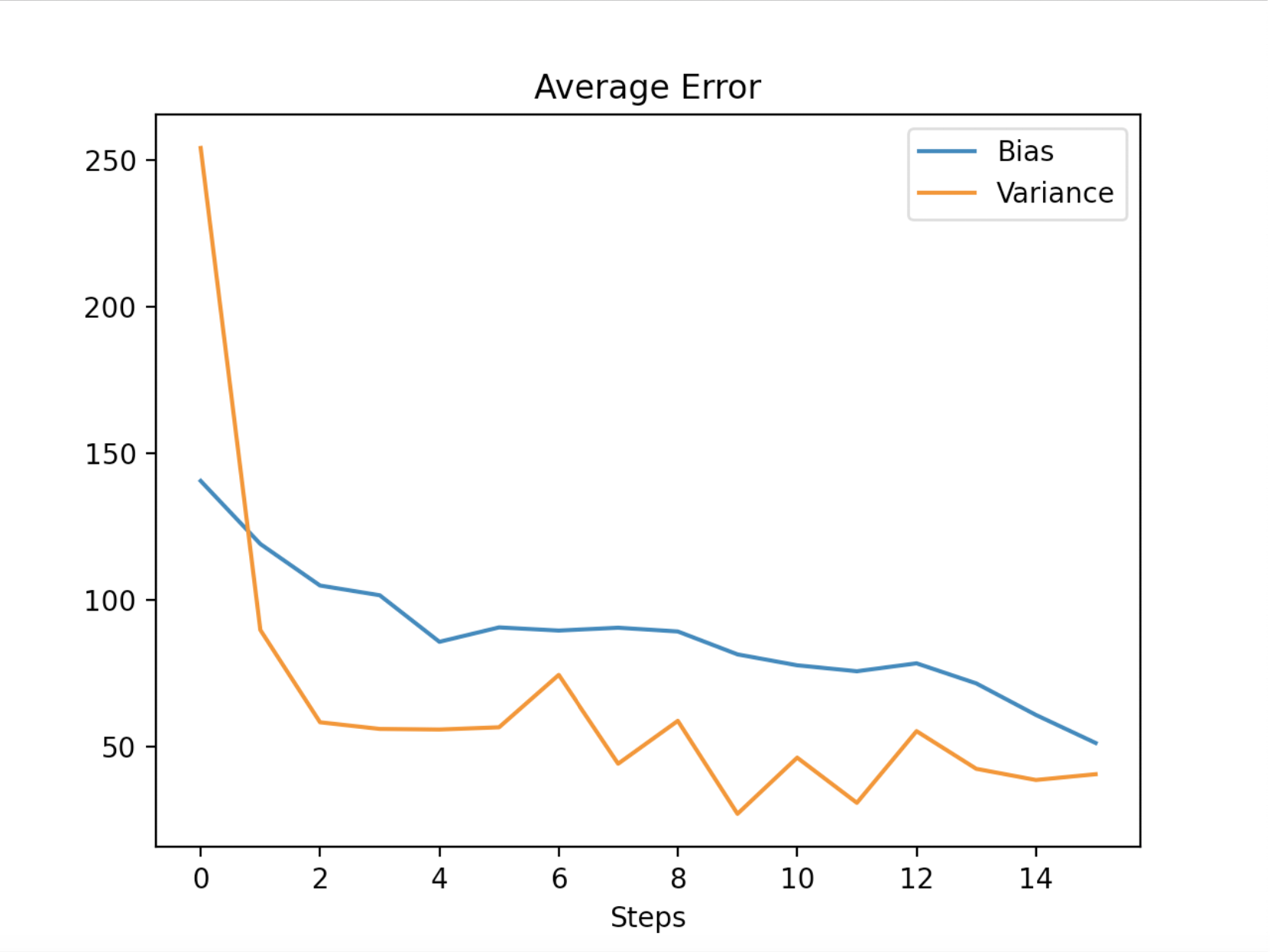
虽然偏差和方差仍可能减少,但我对它们下降的速度并不完全满意。我希望第5步的偏差小于1。
优化
第一个改进的想法是最简单的,增加粒子数量。首先,我想尝试将粒子数增加一倍至1000。让我们来看看?Euro™‘s是如何运行的。
将粒子数增加一倍
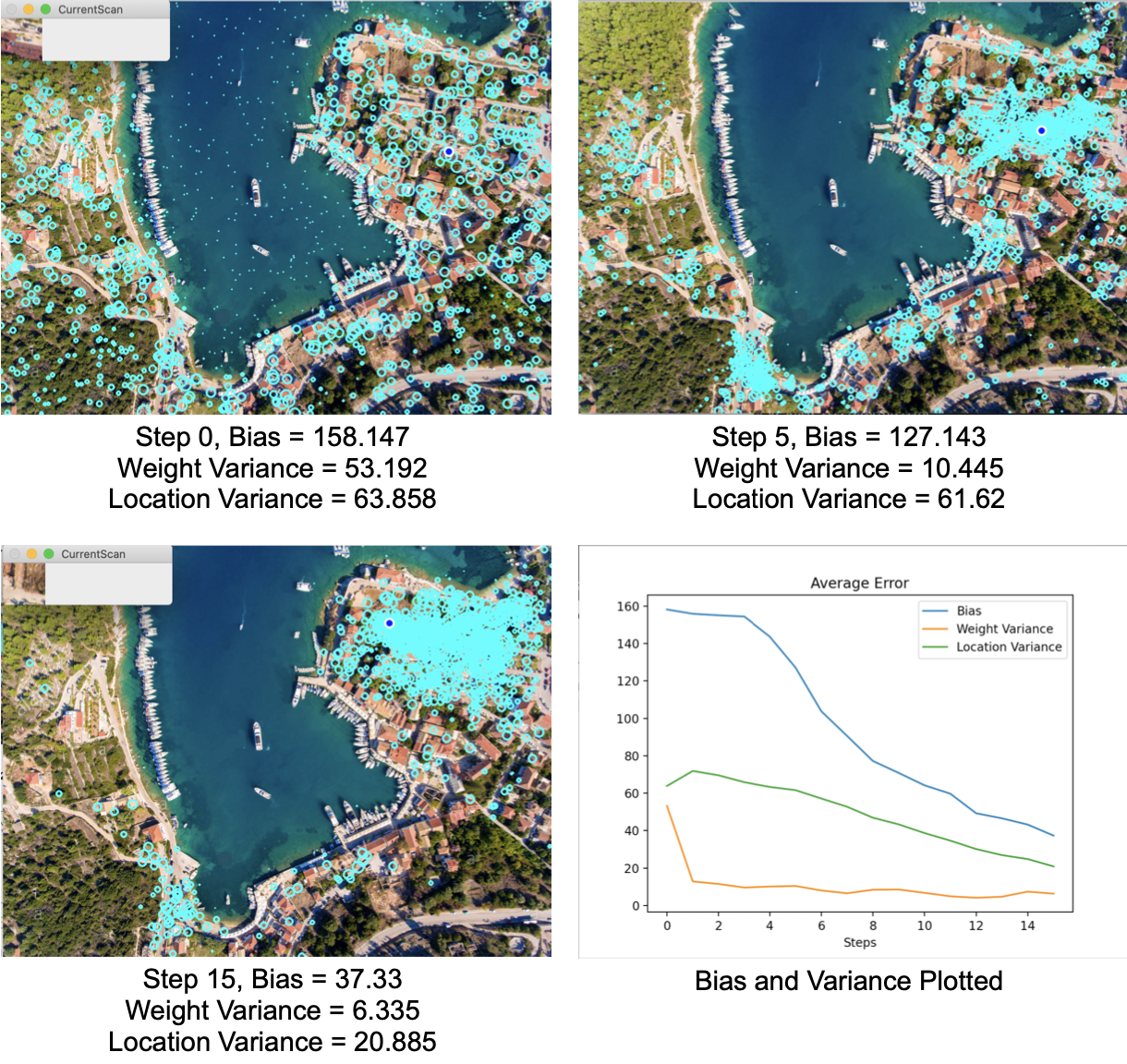
所以这里的结果不言而喻。我们已经减少了方差和偏差。但是我们还没有把粒子定域化。,™。我们或多或少地确定粒子在东部的城镇部分,但是我们不知道它在这个城镇的什么地方。,™,我们不知道它在这个城镇的什么地方。我们基本上已经把它定位到整个小镇了。我认为我们需要增加过滤欧元™的图像识别算法。对于这一点,我有两个想法要实现。
首先,我想使用关联,而不是交集。它对半匹配比完全匹配产生更大的方差,我将增加直方图箱的数量,以便为每个数学提供更多的数据。从理论上讲,这应该会提高所有预测的准确性。
RGB直方图相关性和直方图箱的增加
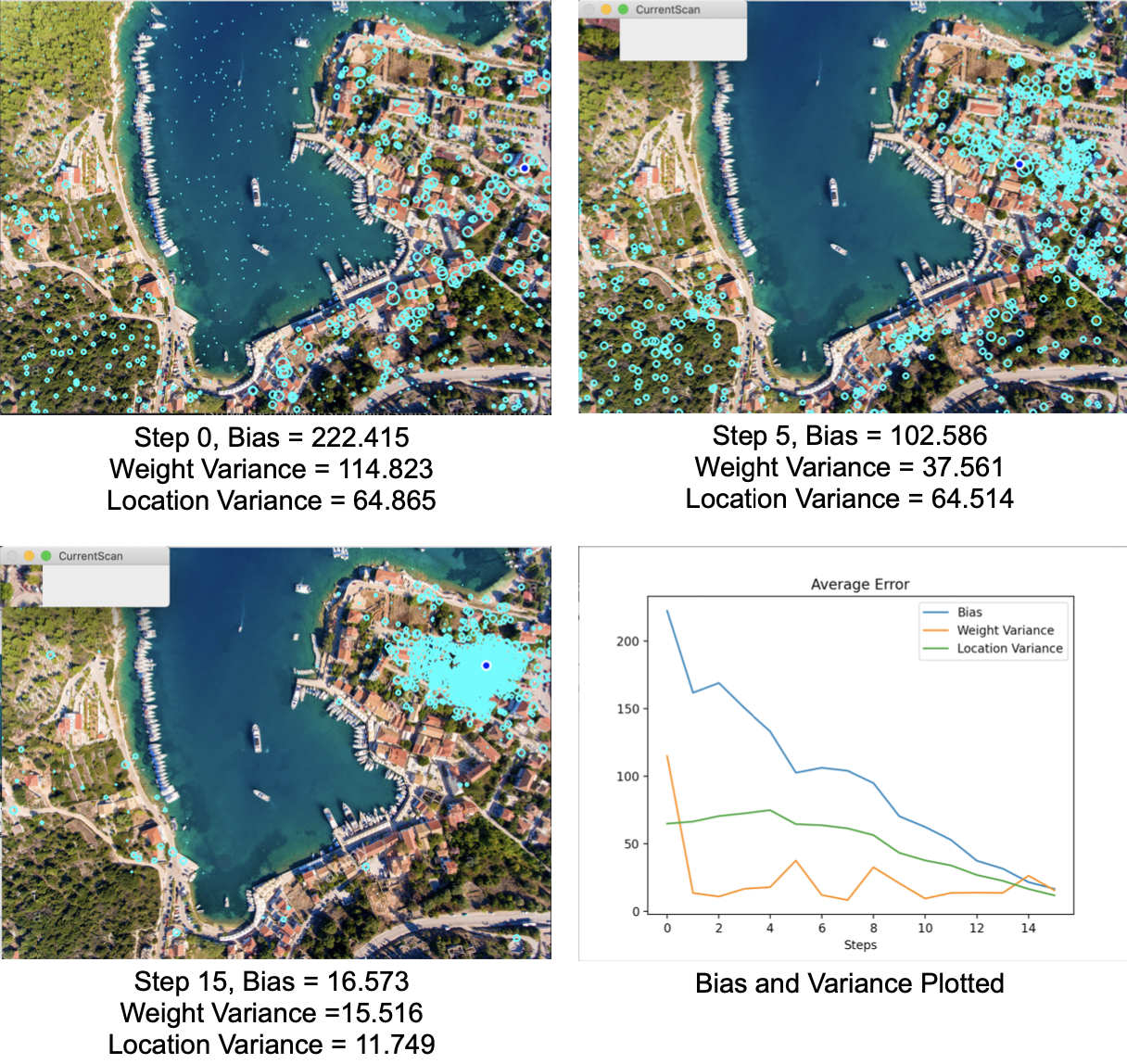
在使用相关性和每个颜色通道更多的条柱(16个而不是8个)之后,图像识别变得更加严格。方差略有下降,偏差也下降了不少,但没有我希望的那么大。我们已经定位到更远的城镇,但偏差仍然太大,我们无法确定无人机在哪里。这里我想试着平方权重,这将增加对比度,从而增加权重之间的差异,但应该使粒子重新生成更加严格。我估计这将去除城外的低重量粒子。
平方重量

这产生的影响比我预期的要大得多。但是,增加粒子中的方差以影响重采样功能可以在总体偏移中产生巨大的差异,这一点很能说明问题。最初可以看到方差和偏差是如何增加的,但一旦做出了良好的选择,偏差和偏差就会下降,很快就会消除较低的排名权重。我对这一进展感到非常高兴,但我有更多的想法,看看是否可以提高偏差减少的速度。我还是想通过第5步击败1的偏差。
我要看看是否可以通过手动移除粒子来消除一些噪音。实际上,移除这些粒子会产生一种可能性,我们最终会得到0个粒子。相反,一旦我们规格化粒子,我会将最低的25%的粒子设置为权重0,这样它们就会被重新采样算法自动移除。
最小粒子量截止值
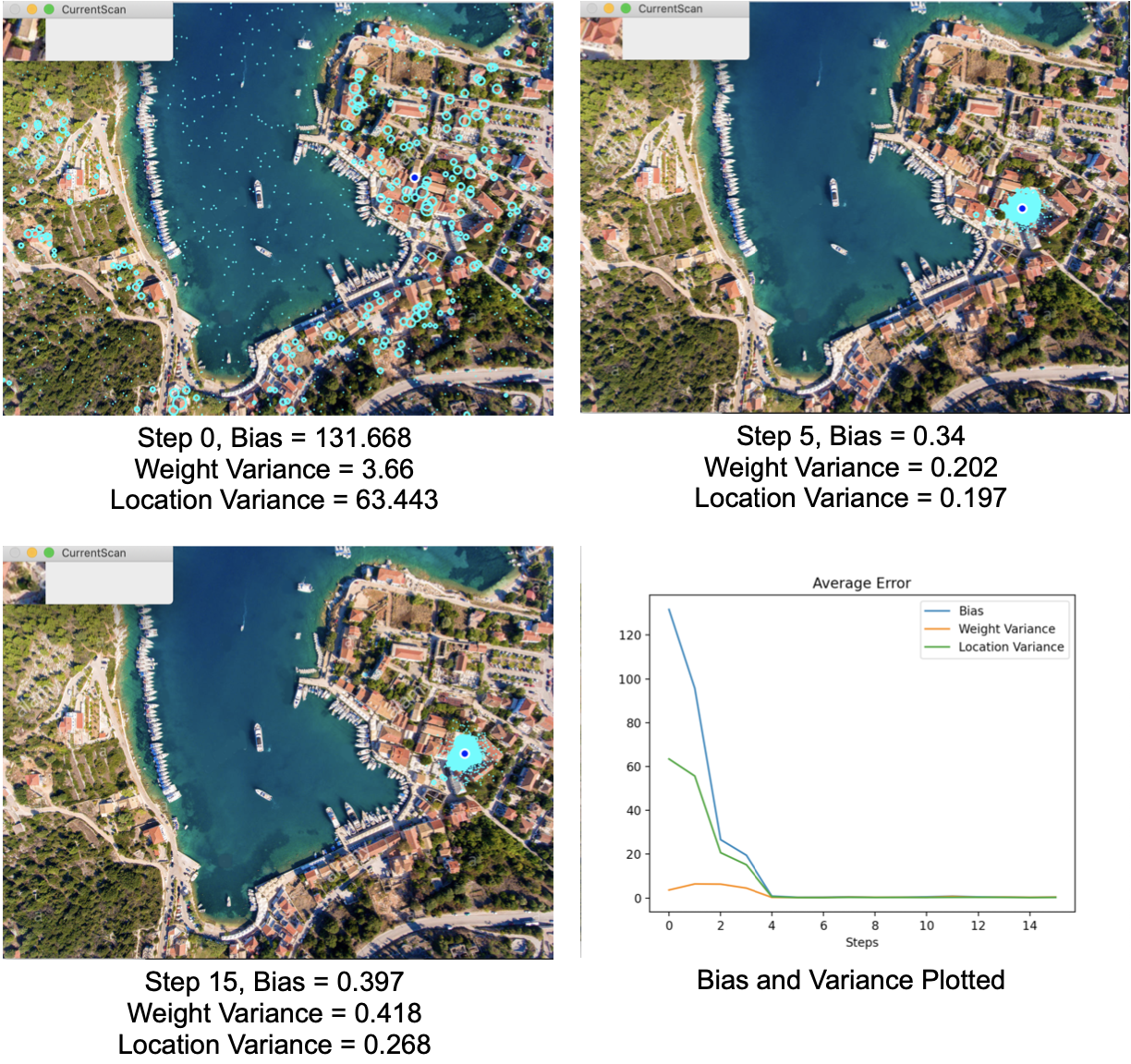
这是快速本地化的最后一个关键。它快速去除了低权重的粒子,并且在4个步骤中偏差下降到接近0。粒子的质量中心离无人机很近。方差也比任何其他方法都低,事实上,我不认为方差会因为重采样噪声而变得更低,因为重采样噪声本身的方差为1。™。所以当然,我想接下来要做的就是限制重采样的噪音。
较低的重采样噪声
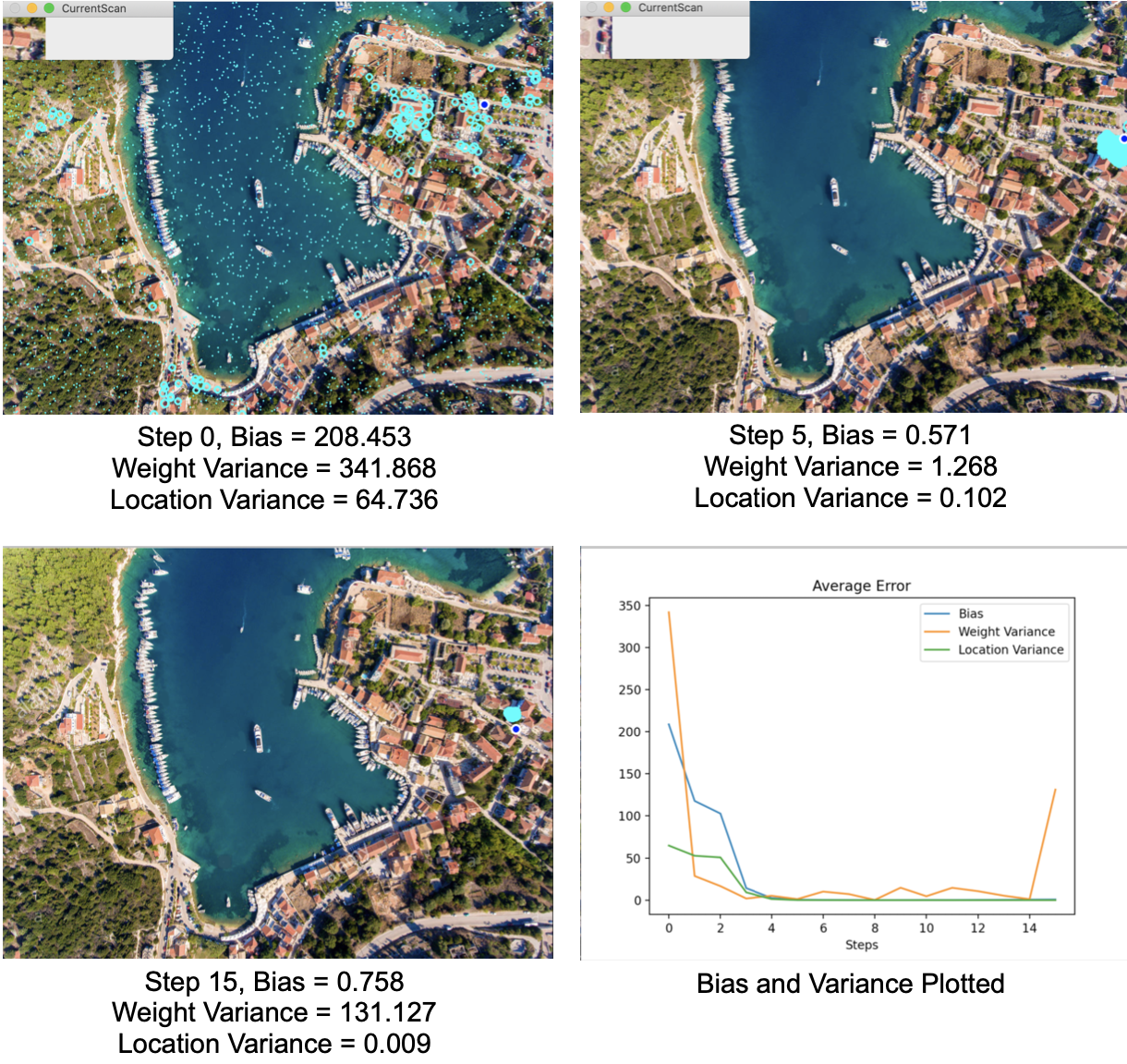
这是我第一次认为这些调整产生了不利影响。我们的偏差比上一个例子高得多,但更重要的是,我不得不将粒子数量增加两倍,这不利于过滤的性能,可能会使其无法实时运行。我之所以这样做,是因为重采样的方差太小了,所以如果无人机的位置从它正下方的粒子开始,我们才会找到它的位置,而且可能会失去无人机,因为无人机速度噪音可能与重新采样噪音的量级相同。在现实世界的解决方案中,我可以通过在粒子中心重新生成样本来重新定位无人机,样本的方差与权重方差相关,这充当了不确定性的衡量标准,尽管我没有在这个项目中实现这一功能。
另一个问题是,这些解决方案只在镇上有效。如果我试图在西北部的海洋或森林上做同样的事情,结果会非常不同。我们从不使用这些方法进行本地化。我将重置在此迭代中更改的参数,并显示当我们从海洋开始时会发生什么。
远洋上的结果
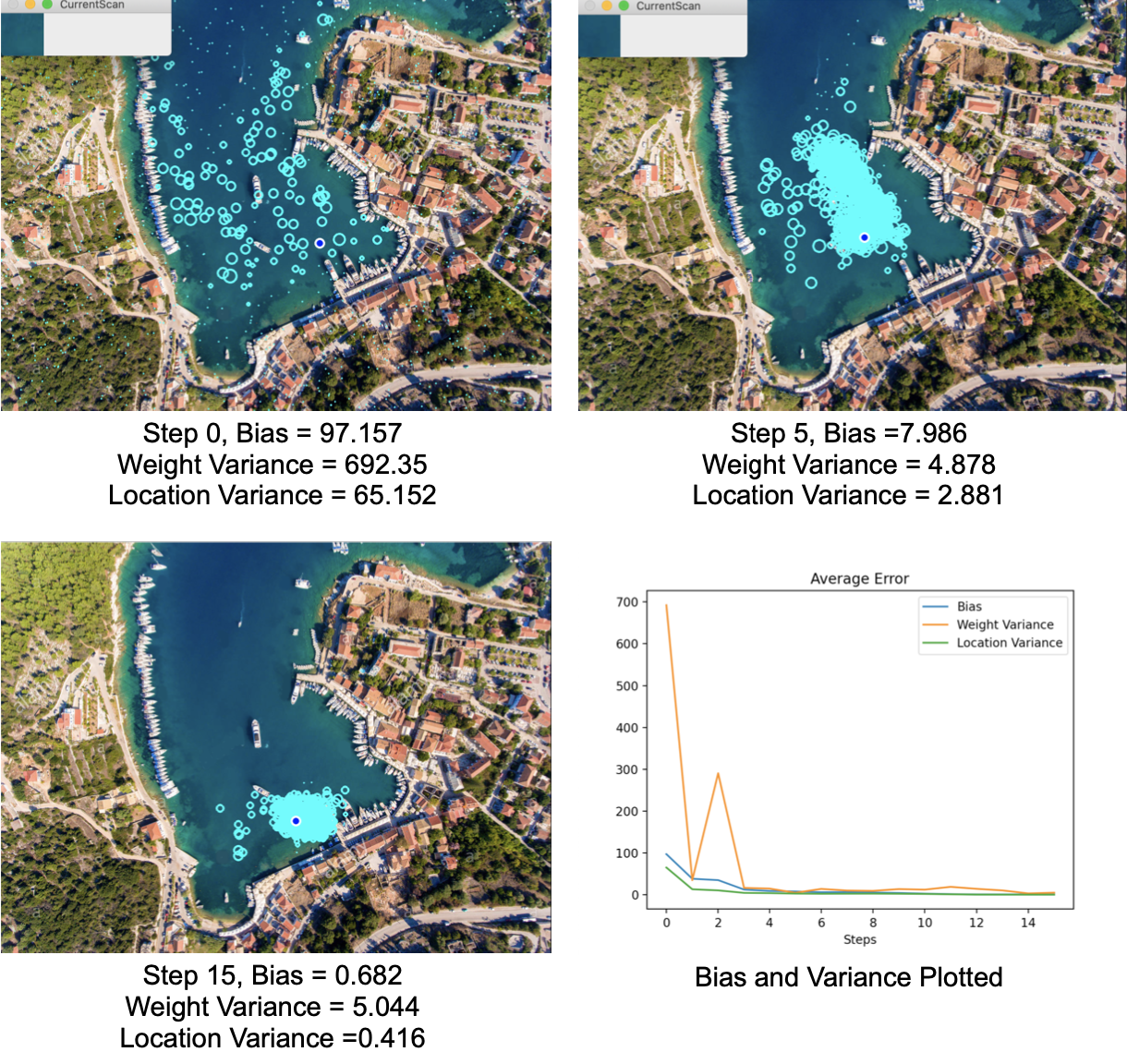
我们从未准确定位过无人机的确切位置。我们确实找到了™所在海域的一般区域,但我认为可以稍作改进。值得注意的是,™的权重变化只有一次降到10以下。当我们做好定位粒子的工作时。我们实际上必须使图像识别变得更灵敏,才能区分相似的蓝色色调。
进一步调谐值

在这最后一次迭代中。我调优了在前面的迭代中引入的一些参数,以使识别在水上工作得非常好。最终参数如下:
-粒子数量:1000-孔径大小:75-重采样噪波=错误·(0,(0.8)*(1?ˆ‘Under‰%)),其中Under‰%是粒子-™重量在所有粒子重量范围内的百分比-粒子截断:Under‰%<60%-无人机移动噪声方差=is.(0,(0.2))-无人机速度幅值=1.0-每个颜色通道的条带数:64 感谢您阅读这篇文章。我鼓励您使用这些策略来优化您自己的粒子过滤器。 另外,请在此处查看我的代码:wilhite-r/ParticleFilterSimulation at 9f476e963bae73e4431ae43b323fad7464fe2720(github.com)所有这些代码都是原始代码,所以如果您使用其中任何代码,请给我发送私人消息。相信我。谢谢!Wilhite-r/ParticleFilterSimulation at 9f476e963bae73e4431ae43b323fad7464fe2720 (github.com)
目录学
[1]Del Moral,Pierre(1996)。?œ非线性滤波:交互粒子解决方案?�。马尔可夫过程及其相关领域。2(4):555?欧元“580.“Non Linear Filtering: Interacting Particle Solutionâ€�
[2]刘俊生;陈荣(1998?EURO“09?EURO”01)。动态系统的序贯蒙特卡罗方法(œ�)。美国统计协会杂志。93(443):1032?欧元“1044.DOI:10.1080/01621459.1998.10473765.ISSN 0162-EURO“1459.doi 10.1080/01621459.1998.10473765 ISSN 0162–1459
[3]Josh Bongard;概率机器人学。塞巴斯蒂安·特龙、沃尔夫拉姆·伯加德和迪特尔·福克斯。(2005,麻省理工学院出版社)647页。艺术生活2008;14(2):227?欧元“229。doi:https://doi.org/10.1162/artl.2008.14.2.227https://doi.org/10.1162/artl.2008.14.2.227
原创文章,作者:fendouai,如若转载,请注明出处:https://panchuang.net/2021/06/18/%e7%94%a8%e7%b2%92%e5%ad%90%e8%bf%87%e6%bb%a4%e6%a8%a1%e6%8b%9f%e6%97%a0%e4%ba%ba%e6%9c%ba%e7%9a%84%e8%87%aa%e5%ae%9a%e4%bd%8d/

