损失函数综述
本文是全系列中第11 / 23篇:TensorFlow 从入门到精通
- Tensorflow 介绍和安装
- 【干货】史上最全的Tensorflow学习资源汇总
- 文末福利|一文上手TensorFlow2.0(一)
- TensorFlow 卷积神经网络手写数字识别数据集介绍
- 特征工程
- 一文上手最新TensorFlow2.0系列(二)
- 深度学习之激活函数
- Tensorflow实现MNIST手写数字识别
- 一文上手Tensorflow2.0之tf.keras|三
- 卷积神经网络概述
- 损失函数综述
- 一文上手Tensorflow2.0(四)
- TensorFlow 一步一步实现卷积神经网络
- Tensorboard 详解(上篇)
- 深度学习发展史
- Tensorflow从入门到精通之——Tensorflow基本操作
- Tensorboard详解(下篇)
- 卷积的发展历程,原理和基于 TensorFlow 的实现
- 五大经典卷积神经网络介绍:LeNet / AlexNet / GoogLeNet / VGGNet/ ResNet
- TensorFlow 多GPU使用详解
- 一文彻底搞懂BP算法:原理推导+数据演示+项目实战(上篇)
- TensorFlow 实战卷积神经网络之 LeNet
- 深度学习之视频人脸识别系列二:人脸检测与对齐
损失函数(loss function)又叫做代价函数(cost function),是用来评估模型的预测值与真实值不一致的程度,也是神经网络中优化的目标函数,神经网络训练或者优化的过程就是最小化损失函数的过程,损失函数越小,说明模型的预测值就越接近真是值,模型的健壮性也就越好。
常见的损失函数有以下几种:
(1) 0-1损失函数(0-1 lossfunction):
0-1损失函数是最为简单的一种损失函数,多适用于分类问题中,如果预测值与目标值不相等,说明预测错误,输出值为1;如果预测值与目标值相同,说明预测正确,输出为0,言外之意没有损失。其数学公式可表示为:
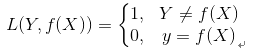
由于0-1损失函数过于理想化、严格化,且数学性质不是很好,难以优化,所以在实际问题中,我们经常会用以下的损失函数进行代替。
(2)感知损失函数(Perceptron Loss):
感知损失函数是对0-1损失函数的改进,它并不会像0-1损失函数那样严格,哪怕预测值为0.99,真实值为1,都会认为是错误的;而是给一个误差区间,只要在误差区间内,就认为是正确的。其数学公式可表示为:
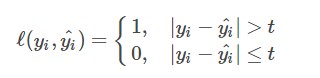
(3)平方损失函数(quadratic loss function):
顾名思义,平方损失函数是指预测值与真实值差值的平方。损失越大,说明预测值与真实值的差值越大。平方损失函数多用于线性回归任务中,其数学公式为:
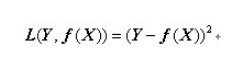
接下来,我们延伸到样本个数为N的情况,此时的平方损失函数为:
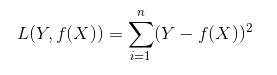
(4)Hinge损失函数(hinge loss function):
Hinge损失函数通常适用于二分类的场景中,可以用来解决间隔最大化的问题,常应用于著名的SVM算法中。其数学公式为:
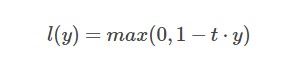
其中在上式中,t是目标值{-1,+1},y为预测值的输出,取值范围在(-1,1)之间。
(5)对数损失函数(Log Loss):
对数损失函数也是常见的一种损失函数,常用于逻辑回归问题中,其标准形式为:
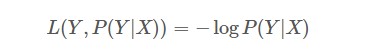
上式中,y为已知分类的类别,x为样本值,我们需要让概率p(y|x)达到最大值,也就是说我们要求一个参数值,使得输出的目前这组数据的概率值最大。因为概率P(Y|X)的取值范围为[0,1],log(x)函数在区间[0,1]的取值为负数,所以为了保证损失值为正数要在log函数前加负号。
(6)交叉熵损失函数(cross-entropy loss function):
交叉熵损失函数本质上也是一种对数损失函数,常用于多分类问题中。其数学公式为:
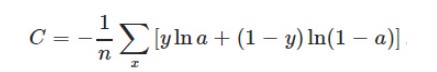
注意:公式中的x表示样本,y代表预测的输出,a为实际输出,n表示样本总数量。交叉熵损失函数常用于当sigmoid函数作为激活函数的情景,因为它可以完美解决平方损失函数权重更新过慢的问题。
以上为大家介绍了较为常见的一些损失函数以及使用场景。接下来的文章中会结合经典的实例——MNIST手写数字识别,为大家讲解如何在深度学习实际的项目中运用激活函数、损失函数。
原创文章,作者:AIxiaoxin,如若转载,请注明出处:https://panchuang.net/2018/05/06/loss/

